Mechanika - Medencefal terhelése
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2014. január 9., 16:46-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*5.7.) Mekkora vízszintes irányú erőt fejt ki a
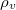 sűrűségű folyadék egy medence függőleges, sík falára, ha a vízmagasság
sűrűségű folyadék egy medence függőleges, sík falára, ha a vízmagasság  , a fal hosszúsága pedig
, a fal hosszúsága pedig  ? Milyen magasságban van az eredő erő támadáspontja?
? Milyen magasságban van az eredő erő támadáspontja?
Megoldás
Az eredő erőt a mélységtől függő hidrosztatiksai nyomás által a felületelemekre kifejtett erőelemek integrálásával kaphatjuk meg. Ugyanígy kapható egy eredő forgatónyomaték nyomatékelemek integrálásával, az eredő erő támadáspontját pedig abból kaphatjuk meg, hogy oda helyezve ezzel megegyező nyomatékot kell adnia. A hidrosztatikai nyomás függése a mélységtől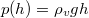 , egy felületelem mérete
, egy felületelem mérete 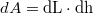 , így egy
, így egy  mélységben található darabkára ható erőelem
mélységben található darabkára ható erőelem 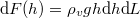 , ebből az eredő erő
, ebből az eredő erő ![\[F_e=\int_0^L\int_0^h\rho_vg\tilde h\text{d}\tilde h\text{d}L=\rho_vgL\frac{h^2}2\]](/images/math/b/e/f/bef387cf7309dd5ad822639e18ce82eb.png)
![\[M_e=\int_0^L\int_0^h\text{d}M(h)=\int_0^L\int_0^h\text{d}F(h)h=\int_0^L\int_0^h\rho_vg\tilde h^2\text{d}\tilde h\text{d}L=\rho_vgL\frac{h^3}3=F_ed,\]](/images/math/7/e/a/7ea5eab265c03618b79ca951f270d646.png)
 a keresett támadáspont. Behelyettesítve az eredő erőt egyszerűsítés után kapjuk:
a keresett támadáspont. Behelyettesítve az eredő erőt egyszerűsítés után kapjuk: 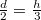 , melyből
, melyből 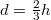 a támadáspont mélysége a vízszinttől (amely magasságtól számítva írtuk fel a nyomatékokat), ez a medence aljától
a támadáspont mélysége a vízszinttől (amely magasságtól számítva írtuk fel a nyomatékokat), ez a medence aljától ![\[\frac h3\]](/images/math/a/e/7/ae7998c299ed89dbc56c73232660d025.png)