Mechanika - Tengerbe lógatott drótkötél
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2013. augusztus 29., 11:33-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.1.) Egy hajóról a
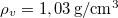 sűrűségű tengerbe lógatnak függőlegesen egy
sűrűségű tengerbe lógatnak függőlegesen egy 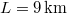 hosszú drótkötelet (keresztmetszete
hosszú drótkötelet (keresztmetszete 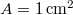 , sűrűsége
, sűrűsége 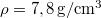 , szakítószilárdsága
, szakítószilárdsága 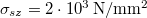 ). Elszakad-e a kötél?
). Elszakad-e a kötél?
Megoldás
A tengerszint alatt mélységben
mélységben 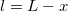 hosszúságú kötéldarab súlya feszíti a kötelet. A felhajtóerő a kötél aljánál ébred, és
hosszúságú kötéldarab súlya feszíti a kötelet. A felhajtóerő a kötél aljánál ébred, és 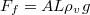 Az eredő feszítő erő
Az eredő feszítő erő  mélységben tehát
mélységben tehát ![\[F(x)=Al\rho g-AL\rho_v g,\]](/images/math/5/0/a/50a22a0c6606d3089659fb72bb24121a.png)
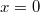 -nál maximális
-nál maximális ![\[F(0)=AL(\rho-\rho_v)g,\]](/images/math/b/f/7/bf794ee4a9950a6c2c458d36c158b667.png)
![\[\sigma=L(\rho-\rho_v)g=0,6\cdot10^9\,\frac{\rm N}{\rm m^2},\]](/images/math/1/c/6/1c643ad92609c02c7c9796a5049f5dce.png)