Erőtan II. - 6.7

Feladat

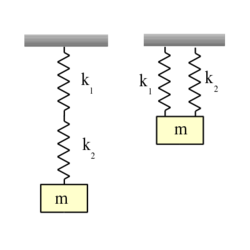
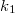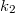1. (6.7) Határozzuk meg a nehézségi erőtérben, az ábrán látható módon a $\setbox0\hbox{$k_{1}$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$k_{2}$}% \message{//depth:\the\dp0//}% \box0%$ direkciós erejű rugókra erősített $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test rezgési frekvenciáit!
   

Megoldás

1. A sorba kötött rugók helyettesíthetők egyetlen rugóval, melynek direkciós állandója

   $\[k=\frac{1}{\frac{1}{k_{1}}+\frac{1}{k_{2}}}\,.\]$

   A rezgés frekvenciája ekkor

   $\[\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{k_{1}k_{2}}{m(k_{1}+k_{2})}}\,.\]$

   Párhuzamos csatolás esetén

   $\[k=k_{1}+k_{2}\,,\]$

   így

   $\[\omega=\sqrt{\frac{k_{1}+k_{2}}{m}}\,.\]$