Erőtan II. - 2.1.23
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2014. január 9., 16:29-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (**2.1.23) Milyen magasra emelkedik egy
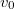 sebességgel függőlegesen felhajított test, ha a sebességgel arányos fékező erő (
sebességgel függőlegesen felhajított test, ha a sebességgel arányos fékező erő (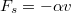 ) hat rá? Mennyi idő alatt éri el a pálya legmagasabb pontját?
) hat rá? Mennyi idő alatt éri el a pálya legmagasabb pontját?
Megoldás
- A testre csak a függőlegesen lefelé irányított gravitációs és a függőlegesen felfelé irányított közegellenállási erők hatnak. A mozgásegyenlet tehát alakban írható.A mozgás az
![\[ma=-mg-\alpha v\]](/images/math/b/0/2/b02fba214baf6269ddbe92afd8dd9ed9.png)
 -tengely mentén történik, amelyet úgy irányítunk, hogy a pozitív vége függőlegesen felfelé mutat. A gyorsulás a sebességnek az idő szerinti deriváltja, így a mozgásegyenlet matematikai szempontból egy elsőrendű, lineáris differenciálegyenlet a sebességre vonatkozóan. A differenciálegyenletet kell
-tengely mentén történik, amelyet úgy irányítunk, hogy a pozitív vége függőlegesen felfelé mutat. A gyorsulás a sebességnek az idő szerinti deriváltja, így a mozgásegyenlet matematikai szempontból egy elsőrendű, lineáris differenciálegyenlet a sebességre vonatkozóan. A differenciálegyenletet kell![\[\dot{v}=-g-\frac{\alpha}{m}v\]](/images/math/5/6/3/5639e756b60091f74353ec12fc6a97e1.png)
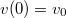 kezdő feltétel mellett megoldani. Legyen
kezdő feltétel mellett megoldani. Legyen![\[\dot{v}=-\frac{\alpha}{m}\left(v+\frac{gm}{\alpha}\right)\]](/images/math/7/2/d/72d34649338c773019a822645c927335.png)
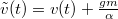 ! Ezzel melynek megoldása
! Ezzel melynek megoldása![\[\dot{\tilde{v}}=-\frac{\alpha}{m}\tilde{v}\,,\]](/images/math/8/8/c/88c95a70109f2495fb3db1172f8e0bb7.png) tetszőleges
tetszőleges![\[\tilde{v}(t)=Ae^{-\frac{\alpha}{m}t}\]](/images/math/a/9/a/a9af0d2bf7dc14ae98ff65107edaf491.png)
 konstanssal, melyet majd a kezdeti feltétel segítségével tudunk meghatározni. A kezdeti feltétel
konstanssal, melyet majd a kezdeti feltétel segítségével tudunk meghatározni. A kezdeti feltétel![\[v(t)=Ae^{-\frac{\alpha}{m}t}-\frac{gm}{\alpha}\]](/images/math/b/f/b/bfb597278311c3a3cd29af7362cc13aa.png)
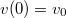 . Ez csak úgy tud teljesülni, ha Így a test sebessége az idő függvényében
. Ez csak úgy tud teljesülni, ha Így a test sebessége az idő függvényében![\[A=v_{0}+\frac{gm}{\alpha}\,.\]](/images/math/5/f/e/5fe79e72efa96745a83a1b22d9383ef2.png) a test helyzete pedig az
a test helyzete pedig az![\[v(t)=\left(v_{0}+\frac{gm}{\alpha}\right)e^{-\frac{\alpha}{m}t}-\frac{gm}{\alpha}\,,\]](/images/math/f/0/a/f0a6bdf377d72b0fa9c0566734c47210.png)
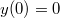 kezdeti feltétellel
kezdeti feltétellel ![\[y(t)=y(0)+\int_{0}^{t}v(t')dt'=-\frac{gm}{\alpha}t+\left(v_{0}+\frac{gm}{\alpha}\right)\frac{m}{\alpha}\left(1-e^{-\frac{\alpha}{m}t}\right)\,.\]](/images/math/2/e/0/2e0248e9b5d9a79008f2ea120cab604f.png)
A test sebessége a megállás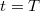 pillanatáig csökken. Ebben a pillanatban
pillanatáig csökken. Ebben a pillanatban 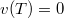 . A test helyzete ebben a pillanatban
. A test helyzete ebben a pillanatban![\[\left(v_{0}+\frac{gm}{\alpha}\right)e^{-\frac{\alpha}{m}T}-\frac{gm}{\alpha}=0\qquad\Rightarrow\qquad T=\frac{m}{\alpha}\ln\left(1+\frac{\alpha v_{0}}{gm}\right)\]](/images/math/0/4/b/04b088e49ce415b7fe08c5f4d899e77e.png) Megjegyezzük, hogy közegellenállásmentes esetben ez a képlet is visszaadja a jól ismert eredményt, ha kihasználjuk, hogy kis
Megjegyezzük, hogy közegellenállásmentes esetben ez a képlet is visszaadja a jól ismert eredményt, ha kihasználjuk, hogy kis![\[y(T)=\frac{mv_{0}}{\alpha}-g\left(\frac{m}{\alpha}\right)^{2}\ln\left(1+\frac{\alpha v_{0}}{gm}\right)\,.\]](/images/math/3/5/2/35231011447a784700938ddcaa2b2263.png)
 -re
-re 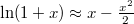 .
. ![\[\alpha\rightarrow 0\mbox{ :}\qquad y(T)=\frac{mv_{0}}{\alpha}-g\left(\frac{m}{\alpha}\right)^{2}\left[\frac{\alpha v_{0}}{gm}-\frac{1}{2}\left(\frac{\alpha v_{0}}{gm}\right)^{2}\right]=\frac{v_{0}^{2}}{2g}\]](/images/math/3/3/f/33fe63de38c54280064c65f156088674.png)
- A testre csak a függőlegesen lefelé irányított gravitációs és a függőlegesen felfelé irányított közegellenállási erők hatnak. A mozgásegyenlet tehát