Mechanika - Rugalmas energia sűrűsége
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. november 15., 16:25-kor történt szerkesztése után volt.
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.3.) Egy eredetileg
 hosszúságú,
hosszúságú,  keresztmetszetű,
keresztmetszetű,  Young-modulusú huzalt a rugalmassági határon belül
Young-modulusú huzalt a rugalmassági határon belül  ? rugalmas feszültséggel terhelünk. Mennyi a huzalban tárolt rugalmas energia térfogati sűrűsége?
? rugalmas feszültséggel terhelünk. Mennyi a huzalban tárolt rugalmas energia térfogati sűrűsége?
Megoldás
A teljes huzalban tárolt rugalmas energia a huzal "rugóállandójával" és teljes megnyúlásával kifejezve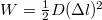 . A rugóállandó függ a huzal geomteriájától és anyagától - azaz Young-modulusától -, a megnyúlás pedig a feszültséggel hozható kapcsolatba. Mivel a Hooke-törvény
. A rugóállandó függ a huzal geomteriájától és anyagától - azaz Young-modulusától -, a megnyúlás pedig a feszültséggel hozható kapcsolatba. Mivel a Hooke-törvény ![\[\sigma=\frac FA=E\frac{\Delta l}L,\]](/images/math/d/b/4/db41ab5b3292466232686fc3addaa75e.png)
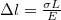 , másrészt
, másrészt ![\[F=\frac{AE}L\Delta l=D\Delta l,\]](/images/math/7/9/f/79f510e8b448ae86297007c2d9d33177.png)
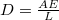 . Ezeket beírva a rugalmas energia kifejezésébe
. Ezeket beírva a rugalmas energia kifejezésébe ![\[W=\frac{AL\sigma^2}{2E},\]](/images/math/e/3/f/e3f594d23f93baba96438ae2338ebd13.png)
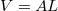 térfogattal leosztva kapjuk
térfogattal leosztva kapjuk ![\[w_r=\frac{\sigma^2}{2E}\]](/images/math/a/6/3/a6395c9caa48cb1694e7fbd9a9bad949.png)