Mechanika - Kifolyás sebessége
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. november 21., 16:30-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.12.) Egy magas, nagy
 keresztmetszetű, vízzel teli edény oldalán, az aljához közel, kis
keresztmetszetű, vízzel teli edény oldalán, az aljához közel, kis 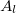 felületű lyukon folyik ki a víz. Az edény keresztmetszete sokkal nagyobb a lyukénál, a víz magassága a lyuk fölött
felületű lyukon folyik ki a víz. Az edény keresztmetszete sokkal nagyobb a lyukénál, a víz magassága a lyuk fölött  . Milyen sebességgel hagyja el a víz a lyukat, ha a folyadék súrlódásmentesen mozog?
. Milyen sebességgel hagyja el a víz a lyukat, ha a folyadék súrlódásmentesen mozog?
Megoldás
A térfogatáram állandósága![\[A_lv=Av_0,\]](/images/math/7/b/e/7be5b105eaed0cc7fa919baa510d4ae6.png)
![\[\frac12\rho v^2=\frac12\rho v_0^2+\rho gh\]](/images/math/3/a/b/3ab79ec5aa3fb1e5c0d0ddba1c3b2985.png)
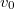 -t kiejtve kapjuk:
-t kiejtve kapjuk: ![\[v=\sqrt{\frac{2gh}{1-\frac{A_l^2}{A^2}}}\approx\sqrt{2gh}\]](/images/math/2/5/b/25b631ea442c582b226bd559eedbc0ba.png)