Mechanika - Lamináris áramlás
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. november 21., 16:33-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.13.) Vízszintes helyzetű, párhuzamos síklemezek között
 vastagságú folyadékréteg van. A felső lemezt
vastagságú folyadékréteg van. A felső lemezt 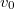 állandó sebességgel mozgatjuk, az alsó lemez nyugalomban van. Mekkora a mozgó lemeztől
állandó sebességgel mozgatjuk, az alsó lemez nyugalomban van. Mekkora a mozgó lemeztől  távolságban a folyadék sebessége?
távolságban a folyadék sebessége?
Megoldás
Feltéve, hogy az áramlás lamináris, az áramlási sebesség a lemezektől mért távolságnak lineáris függvénye, tehát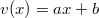 , ahol
, ahol  a mozgó lemeztől mért távolság, és a peremfeltételek
a mozgó lemeztől mért távolság, és a peremfeltételek 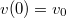 , valamint
, valamint 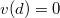 . Ezekből
. Ezekből ![\[v(x)=v_0\left(1-\frac xd\right)\]](/images/math/4/3/d/43d155e4cf68b11100bff2cc4aa1fb52.png)