Erőtan II. - 4.13
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 22., 20:39-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- ÁBRA Egy liftben
 direkciós erejű rugóra erősítve egy
direkciós erejű rugóra erősítve egy  tömegű testet függesztünk fel. A test a
tömegű testet függesztünk fel. A test a 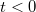 időpontokban nyugalomban van. A lift a
időpontokban nyugalomban van. A lift a  időpontban
időpontban 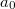 gyorsulással emelkedni kezd. (4.13. ábra)
gyorsulással emelkedni kezd. (4.13. ábra) 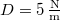 ,
, 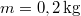 ,
, 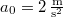 .
.
- a) Milyennek észleli a test mozgását a liftbeli megfigyelő?
- b) Külön ábrán jelölje be az m tömegű testre - a gyorsuló lift koordinátarendszerében - ható erőket, és írja fel a test mozgásegyenletét az ábrán bejelölt (lifthez rögzített) koordinátarendszerben!
- c) Határozza meg a test mozgását jellemző
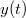 függvényt, ha a test az ábra szerinti
függvényt, ha a test az ábra szerinti 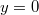 koordinátájú pontban történő elhelyezkedése a
koordinátájú pontban történő elhelyezkedése a 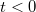 időpontokban fennálló egyensúlyi állapotra érvényes! (Az
időpontokban fennálló egyensúlyi állapotra érvényes! (Az 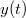 függvény jellemző mennyiségeit számszerűen adja meg!)
függvény jellemző mennyiségeit számszerűen adja meg!)
Megoldás
- a) A gyorsulás hatására a lifthez rögzített vonatkoztatási rendszerben a testre hat egy függőleges irányú és
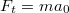 nagyságú tehetetlenségi erő. Ennek hatására a test a rugón rezegni kezd.
nagyságú tehetetlenségi erő. Ennek hatására a test a rugón rezegni kezd.
- b) A mozgásegyenlet a lift koordináta-rendszerében ahol a rugó megnyúlása
![\[m\ddot{y}=D\Delta l-mg-F_{t}\,,\]](/images/math/8/d/1/8d197b7ac6f376c316064115c2baa8ce.png)
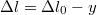 szerint függ össze a test helyzetével. Az egyensúlyi helyzetben (
szerint függ össze a test helyzetével. Az egyensúlyi helyzetben (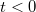 ) a megnyúlás
) a megnyúlás 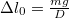 volt. Így a mozgásegyenlet
volt. Így a mozgásegyenlet ![\[m\ddot{y}=-Dy-ma_{0}\,.\]](/images/math/3/4/4/34454d0d19d8ed83ab73829f1cd00ad8.png)
- c)
- a) A gyorsulás hatására a lifthez rögzített vonatkoztatási rendszerben a testre hat egy függőleges irányú és
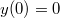 és
és 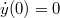 kezdeti feltételek mellett kell megoldani.
kezdeti feltételek mellett kell megoldani. ![\[\ddot{y}+\omega^{2}(y-y_{0})=0\qquad \omega=\sqrt{\frac{D}{m}}=5\frac{1}{\,\mathrm{s}}\qquad y_{0}=-\frac{ma_{0}}{D}=-0,08\,\mathrm{m}\]](/images/math/2/a/3/2a3e6fd304215d2a14978bc5ea989cef.png)
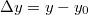 -ra vonatkozó
-ra vonatkozó 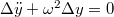 differenciálegyenlet két független megoldása
differenciálegyenlet két független megoldása 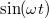 és
és 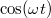 , így
, így ![\[y(t)=y_{0}+A\sin(\omega t)+B\cos(\omega t)\,,\]](/images/math/c/e/a/cea66346fc0a7a38157c411f1be38dbf.png)
 és
és  paramétereket a kezdeti feltételek segítségével kell maghatározni.
paramétereket a kezdeti feltételek segítségével kell maghatározni. ![\[0=y(0)=y_{0}+B\qquad\Rightarrow\qquad B=-y_{0}\]](/images/math/2/2/6/2262fc0bbf4016c545f96aaf7e0434a6.png)
![\[0=\dot{y}(0)=A\omega\qquad\Rightarrow \qquad A=0\]](/images/math/3/b/6/3b6564df8fcc98b5eede1e87d80f8905.png)
![\[y(t)=y_{0}(1-\cos(\omega t))\,.\]](/images/math/9/2/5/925b4cce2bb2f478743e0c7b34da2fa0.png)