Mechanika - Rétegezett folyadékok
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.5.) Egy edényben lévő
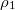 sűrűségű folyadék fölé
sűrűségű folyadék fölé 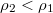 sűrűségű folyadékot rétegeznek. A két folyadék határán egy
sűrűségű folyadékot rétegeznek. A két folyadék határán egy  térfogatú,
térfogatú,  sűrűségű test lebeg. A test térfogatának mekkora része merül a nagyobb sűrűségű folyadékba?
sűrűségű test lebeg. A test térfogatának mekkora része merül a nagyobb sűrűségű folyadékba?
Megoldás
Legyen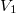 az alsó folyadékba bemerülő rész térfogata,
az alsó folyadékba bemerülő rész térfogata, 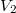 a felső folyadékrétegben lévőé, és
a felső folyadékrétegben lévőé, és 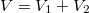 az összes térfogat. A súlyerő
az összes térfogat. A súlyerő ![\[F=\rho(V_1+V_2)g,\]](/images/math/e/4/3/e439ff3c1d0056b72a0218d74a9fceb9.png)
![\[F_{fel}=\rho_2V_2g+\rho_1V_1g,\]](/images/math/5/9/5/5952af811f6b2c5a3dd085b7d8bc5bc5.png)
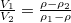 . A teljes térfogathoz viszonyított arányhoz:
. A teljes térfogathoz viszonyított arányhoz: ![\[V=V_1+V_1\frac{V_2}{V_1}=V_1\left(1+\frac{V_2}{V_1}\right)\]](/images/math/5/5/0/550a3bad22ada768928d3c537d0537ba.png)
![\[V_1=\frac{\rho-\rho_2}{\rho_1-\rho_2}V\]](/images/math/b/f/c/bfc2c6407da74462e2d00e2a30c28456.png)