„Erőtan II. - 6.10” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Erőtan II. {{Kísérleti fizika gyakorlat …”) |
|||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Síklemez a rajta nyugvó testtel együtt harmonikus rezgést végez a vízszintes síkban. A rezgés amplitúdója $A=10\,\ | + | </noinclude><wlatex># (6.10.) Síklemez a rajta nyugvó testtel együtt harmonikus rezgést végez a vízszintes síkban. A rezgés amplitúdója $A=10\,\rm{cm}$. Mekkora a lemez és a test közötti súrlódási együttható, ha a test akkor kezd csúszni a lemezen, amikor a rezgésidő kisebb lesz, mint $T=1\,\rm{s}$?</wlatex><includeonly><wlatex>{{Útmutatás|content=A lemezen lévő testet vízszintesen csak a súrlódási erő mozgatja.}}{{Végeredmény|content=$$\mu=0,402$$}}</wlatex></includeonly><noinclude> |
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content=$\mu=0, | + | |
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Ha a rezgésidő $T$, a rezgés körfrekvenciája $\omega=\frac{2\pi}T$, és a test legnagyobb gyorulása $a_{max}=\omega^2A$. Mivel a testre vízszintesen csak a súrlódási erő hat, a test mozgásegyenlete $ma=F_s$. A kritikus pillanat az, amikor a gyorulás a legnagyobb, ekkor a súrlódási erő nem lehet nagyobb a tapadási maximumnál, azaz $$ma_{max}=mA\omega^2=F_{s,max}=\mu mg,$$ mivel a nyomóerő ebben az esetben a nehézségi erővel egyezik meg. Ebből rendezés után $$\mu=\frac{A4\pi^2}{gT^2}=0,402$$</wlatex> |
| − | </wlatex> | + | |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 28., 13:58-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (6.10.) Síklemez a rajta nyugvó testtel együtt harmonikus rezgést végez a vízszintes síkban. A rezgés amplitúdója
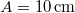 . Mekkora a lemez és a test közötti súrlódási együttható, ha a test akkor kezd csúszni a lemezen, amikor a rezgésidő kisebb lesz, mint
. Mekkora a lemez és a test közötti súrlódási együttható, ha a test akkor kezd csúszni a lemezen, amikor a rezgésidő kisebb lesz, mint 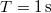 ?
?
Megoldás
Ha a rezgésidő , a rezgés körfrekvenciája
, a rezgés körfrekvenciája 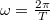 , és a test legnagyobb gyorulása
, és a test legnagyobb gyorulása 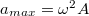 . Mivel a testre vízszintesen csak a súrlódási erő hat, a test mozgásegyenlete
. Mivel a testre vízszintesen csak a súrlódási erő hat, a test mozgásegyenlete 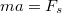 . A kritikus pillanat az, amikor a gyorulás a legnagyobb, ekkor a súrlódási erő nem lehet nagyobb a tapadási maximumnál, azaz
. A kritikus pillanat az, amikor a gyorulás a legnagyobb, ekkor a súrlódási erő nem lehet nagyobb a tapadási maximumnál, azaz ![\[ma_{max}=mA\omega^2=F_{s,max}=\mu mg,\]](/images/math/7/c/e/7ce86d60118c0d80e179c152263cec52.png)
![\[\mu=\frac{A4\pi^2}{gT^2}=0,402\]](/images/math/2/5/3/253be9b3a0d024cb658be66d40eacfa2.png)