Mechanika - Rángatott rugó

Feladat

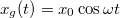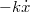1. (6.34.) $\setbox0\hbox{$D$}% \message{//depth:\the\dp0//}% \box0%$ direkciós erejű rugó felfüggesztési pontja $\setbox0\hbox{$x_g(t)=x_0\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%$ szerint mozog. A rugóra függesztett $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test súrlódó közegbe nyúlik, ezért $\setbox0\hbox{$-k\dot x$}% \message{//depth:\the\dp0//}% \box0%$ fékező erő hat rá. Mekkora a test stacionárius rezgéseinek amplitúdója?

Megoldás

A test mozgásegyenlete:

$\[m\ddot x=-D(x-x_g)-k\dot x=-Dx+Dx_0\cos\omega t-k\dot x\]$

átosztva a tömeggel és rendezve

$\[\ddot x+\omega_0^2x+2\beta\dot x=\omega_0^2x_0\cos\omega t,\]$

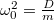ahol $\setbox0\hbox{$\omega_0^2=\frac Dm$}% \message{//depth:\the\dp0//}% \box0%$a csillapítatlan sajátrezgés körfrekvenciája, 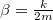$\setbox0\hbox{$\beta=\frac k{2m}$}% \message{//depth:\the\dp0//}% \box0%$ pedig a csillapítási tényező. Ez az egyenlet megfelel az erőgerjesztett kényszerrezgés egyenletének, csak az 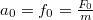$\setbox0\hbox{$a_0=f_0=\frac{F_0}m$}% \message{//depth:\the\dp0//}% \box0%$ gerjesztési (gyorsulás dimenziójú) amplitúdó helyett 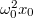$\setbox0\hbox{$\omega_0^2x_0$}% \message{//depth:\the\dp0//}% \box0%$ látható. Innentől a megoldás megfelelő helyettesítéssel azonos az említett esetével, tehát a stacionáius rezgések amplitúdója az $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ gerjesztési frekvencia függvényében

$\[A(\omega)=\frac{\omega_0^2x_0}{\sqrt{(\omega_0^2-\omega^2)^2+(2\beta\omega)^2}}\]$