Mechanika - Rezonanciák
A Fizipedia wikiből
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*6.35.) Csillapított lineáris harmonikus oszcillátort kényszerrezgésbe hozunk. A mozgás folyamán lesz olyan időpont, amikor az oszcillátor sebessége a legnagyobb. Ha megváltoztatjuk a kényszererő frekvenciáját, megváltozik a legnagyobb sebesség értéke is. Hogyan válasszuk meg a kényszerrezgés frekvenciáját, hogy ez a legnagyobb sebesség (mint a frekvencia függvénye) maximális legyen? Mekkora körfrekvenciánál legnagyobb a rezgés amplitúdója?
Megoldás
Ha![\[A(\omega)=\frac{f_0}{\sqrt{(\omega_0^2-\omega^2)^2+(2\beta\omega)^2}}\]](/images/math/1/1/7/1172cb5ada9c8add420dfe116ad7de4b.png)
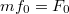 amplitúdójú erőgerjesztés esetén, akkor a sebessségamplitúdó
amplitúdójú erőgerjesztés esetén, akkor a sebessségamplitúdó 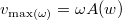 lesz, és ennek keressük a szélsőértékét. Mielőtt azonban nekiállunk deriválni ezt a kifejezést, érdemes megnézni, hogy milyen jellegű. Először is
lesz, és ennek keressük a szélsőértékét. Mielőtt azonban nekiállunk deriválni ezt a kifejezést, érdemes megnézni, hogy milyen jellegű. Először is  értéke közömbös, tehát a továbbiakban 1-nek vesszük. Mivel mind a számláló, mind a nevezőben lévő gyökös kifejezés pozitív, kereshetjük a reciprok szélsőértékét, lévén az
értéke közömbös, tehát a továbbiakban 1-nek vesszük. Mivel mind a számláló, mind a nevezőben lévő gyökös kifejezés pozitív, kereshetjük a reciprok szélsőértékét, lévén az  szigorúan monoton függvény. Hasonló okokból a kérdéses tört négyzetének a szélsőértékét is kereshetjük, mivel az
szigorúan monoton függvény. Hasonló okokból a kérdéses tört négyzetének a szélsőértékét is kereshetjük, mivel az  függvény pozitív argumentumú szakasza is szigorúan monoton. Végső soron tehát elegendő az
függvény pozitív argumentumú szakasza is szigorúan monoton. Végső soron tehát elegendő az ![\[\frac1{A^2\omega^2}=\frac{(\omega_0^2-\omega^2)^2+(2\beta\omega)^2}{\omega^2}=\frac{(\omega_0^2-\omega^2)^2}{\omega^2}+4\beta^2\]](/images/math/3/d/1/3d13bb461e9355ae17928fdb2326ace0.png)
 -tól, a szélsőérték helyét nem befolyásolja, az első tag törtje pedig mindenképp pozitív értékű, és
-tól, a szélsőérték helyét nem befolyásolja, az első tag törtje pedig mindenképp pozitív értékű, és 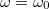 esetén éppen nulla, tehát minimális is, így ez a sebességrezonancia feltétele. Az amplitúdórezonancia helye szintén gyorsan megtalálható, ha egyből
esetén éppen nulla, tehát minimális is, így ez a sebességrezonancia feltétele. Az amplitúdórezonancia helye szintén gyorsan megtalálható, ha egyből 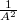 szélsőértékéthelyét keressük:
szélsőértékéthelyét keressük: ![\[\frac{\partial}{\partial\omega}\left((\omega_0^2-\omega^2)^2+4\beta^2\omega^2 \right )=-2(\omega_0^2-\omega^2)2\omega+8\beta^2\omega=0,\]](/images/math/8/5/2/852af2e62fc82c26973e56f5d3853889.png)
![\[\omega^2=\omega_0^2-2\beta^2\]](/images/math/8/c/2/8c2ca743a8704a5982c1076cd2281edc.png)