„Mechanika - Lendkerék fékezése” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
a |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (3.2.3.) Egy $m=50\,\rm{kg}$ és $R=0,5\,\rm m$ sugarú lendítőkerék $600/\rm{perc}$ fordulatszámmal forog. A korong pereme és a féktuskó között a súrlódási együttható 0,5. | + | </noinclude><wlatex># (3.2.3.) Egy $m=50\,\rm{kg}$ és $R=0,5\,\rm m$ sugarú homogén lendítőkerék $600/\rm{perc}$ fordulatszámmal forog. A korong pereme és a féktuskó között a súrlódási együttható 0,5. |
#: a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az $10\, \rm s$ alatt megálljon? | #: a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az $10\, \rm s$ alatt megálljon? | ||
| − | #: b) Mekkora a megállítás ideje alatt a súrlódó erő munkája?</wlatex><includeonly><wlatex>{{Végeredmény|content= | + | #: b) Mekkora a megállítás ideje alatt a súrlódó erő munkája?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$F=157\,\rm{N}$$ $$W_{F_s}=12377\,\rm J=1250\,\pi^2\,\rm J$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A lendkerék tehetetlenségi nyomatéka $\theta_{\rm{TKP}}=\frac12mR^2$, a mozgásegyenlet $\Sigma M=\theta\beta$ ebben az esetben $$\mu FR=\frac12mR^2\beta,$$ továbbá $\omega=2\pi f=\beta t$, így ezekből $$\frac{mR2\pi f}{2\mu t}=157\,\rm N,$$ A súrlódási erő munkája $$W_{F_s}=\mu FR\omega \frac{t}2=\frac12\theta\omega^2=12377\,\rm J=1250\,\pi^2\,\rm J,$$ azaz épp a kezdeti mozgási energiát emészti el.</wlatex> | + | <wlatex>A lendkerék tehetetlenségi nyomatéka $\theta_{\rm{TKP}}=\frac12mR^2$, a mozgásegyenlet $\Sigma M=\theta\beta$ ebben az esetben $$\mu FR=\frac12mR^2\beta,$$ továbbá $\omega=2\pi f=\beta t$, így ezekből $$F=\frac{mR2\pi f}{2\mu t}=157\,\rm N,$$ A súrlódási erő munkája $$W_{F_s}=-\mu FR\omega \frac{t}2=-\frac12\theta\omega^2=-12377\,\rm J=-1250\,\pi^2\,\rm J,$$ azaz épp a kezdeti mozgási energiát emészti el.</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 26., 11:44-kori változata
Feladat
- (3.2.3.) Egy
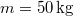és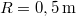 
sugarú homogén lendítőkerék 
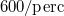fordulatszámmal forog. A korong pereme és a féktuskó között a súrlódási együttható 0,5.
- a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az
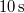alatt megálljon?
- b) Mekkora a megállítás ideje alatt a súrlódó erő munkája?
- a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az
Megoldás
A lendkerék tehetetlenségi nyomatéka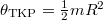
, a mozgásegyenlet 
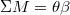ebben az esetben ![\[\mu FR=\frac12mR^2\beta,\]](/images/math/9/3/d/93dd9b1ee053cd0c1597fd0fdbe08c50.png)
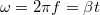, így ezekből ![\[F=\frac{mR2\pi f}{2\mu t}=157\,\rm N,\]](/images/math/2/2/5/225aa82fe2481f217a0d17aabc9f0c0f.png)
![\[W_{F_s}=-\mu FR\omega \frac{t}2=-\frac12\theta\omega^2=-12377\,\rm J=-1250\,\pi^2\,\rm J,\]](/images/math/0/b/a/0ba0bed74fe7fd918c9d89bb11b38b58.png)
