„Pontrendszerek - 3.1.2” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Pontrendszerek {{Kísérleti fizika gyakorl…”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy súrlódásmentes álló csigán átvetett fonálon egy $m_{1}=90 \,\mathrm{g}$ és egy $m_{2}=110\,\mathrm{g}$ tömegű test függ. A nehezebb test a földfelszín felett $H=2\,\mathrm{m}$-re van. Magára hagyva a rendszert, mennyi idő alatt ér le a nagyobb tömegű test a talajra? Feltesszük, hogy a fonál elegendően hosszú. A csiga és a fonál tömegét elhanyagolhatjuk. | + | </noinclude><wlatex># (3.1.2) Egy súrlódásmentes álló csigán átvetett fonálon egy $m_{1}=90 \,\mathrm{g}$ és egy $m_{2}=110\,\mathrm{g}$ tömegű test függ. A nehezebb test a földfelszín felett $H=2\,\mathrm{m}$-re van. Magára hagyva a rendszert, mennyi idő alatt ér le a nagyobb tömegű test a talajra? Feltesszük, hogy a fonál elegendően hosszú. A csiga és a fonál tömegét elhanyagolhatjuk. |
</wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!}}{{Végeredmény|content= $T=2\,\mathrm{s}$ }}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!}}{{Végeredmény|content= $T=2\,\mathrm{s}$ }}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap jelenlegi, 2013. augusztus 27., 22:35-kori változata
Feladat
- (3.1.2) Egy súrlódásmentes álló csigán átvetett fonálon egy
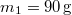 és egy
és egy 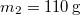 tömegű test függ. A nehezebb test a földfelszín felett
tömegű test függ. A nehezebb test a földfelszín felett 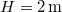 -re van. Magára hagyva a rendszert, mennyi idő alatt ér le a nagyobb tömegű test a talajra? Feltesszük, hogy a fonál elegendően hosszú. A csiga és a fonál tömegét elhanyagolhatjuk.
-re van. Magára hagyva a rendszert, mennyi idő alatt ér le a nagyobb tömegű test a talajra? Feltesszük, hogy a fonál elegendően hosszú. A csiga és a fonál tömegét elhanyagolhatjuk.
Megoldás
- Mindkét testre hat egy gravitációs erő és egy kötélerő. A két kötélerő megegyezik, mert a kötél nyújthatatlan és tömege elhanyagolható, a csiga tömege szintén elhanyagolható. A két test gyorsulásának nagysága is megegyezik, mert a kötél hossza a mozgás során nem változik. A gyorsulások iránya viszont különböző.
![\[m_{1}a=K-m_{1}g\]](/images/math/1/9/0/19053c9a859c99a47a258ede0be3ce02.png) A két egyenletből
A két egyenletből![\[m_{2}a=m_{2}g-K\]](/images/math/3/8/2/382ec00c99e48a6179179e4eb87a9636.png) a testek gyorsulása. A
a testek gyorsulása. A![\[a=\frac{m_{2}-m_{1}}{m_{2}+m_{1}}g\]](/images/math/1/f/0/1f0105f53164f1bca4e96171e5df6ef2.png)
 magasság megtételéhez szükséges idő
magasság megtételéhez szükséges idő ![\[T=\sqrt{\frac{2H}{a}}=\sqrt{\frac{2H}{g}\frac{m_{2}+m_{1}}{m_{2}-m_{1}}}=2\,\mathrm{s}\]](/images/math/9/d/0/9d039630a6d3807333c2a8fae6af15de.png)
- Mindkét testre hat egy gravitációs erő és egy kötélerő. A két kötélerő megegyezik, mert a kötél nyújthatatlan és tömege elhanyagolható, a csiga tömege szintén elhanyagolható. A két test gyorsulásának nagysága is megegyezik, mert a kötél hossza a mozgás során nem változik. A gyorsulások iránya viszont különböző.