„Pontrendszerek - 3.1.16” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Pontrendszerek {{Kísérleti fizika gyakorl…”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Valamely $m_{1}$ tömegű test rugalmatlanul ütközik egy $m_{2}$ tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az $m_{2}$ tömegű test az ütközés előtt nyugalomban volt! | + | </noinclude><wlatex># (3.1.16) Valamely $m_{1}$ tömegű test rugalmatlanul ütközik egy $m_{2}$ tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az $m_{2}$ tömegű test az ütközés előtt nyugalomban volt! |
</wlatex><includeonly><wlatex>{{Útmutatás|content=Tökéletesen rugalmatlan ütközés esetén is érvényes az impulzus megmaradás és a későbbi sebességek azonosak lesznek. Vigyázat! A teljes mozgási energia NEM marad meg az ütközés során!}}{{Végeredmény|content=$$\frac{E_{kin,0}-E_{kin}}{E_{kin,0}}=\frac{m_{2}}{m_{1}+m_{2}}$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=Tökéletesen rugalmatlan ütközés esetén is érvényes az impulzus megmaradás és a későbbi sebességek azonosak lesznek. Vigyázat! A teljes mozgási energia NEM marad meg az ütközés során!}}{{Végeredmény|content=$$\frac{E_{kin,0}-E_{kin}}{E_{kin,0}}=\frac{m_{2}}{m_{1}+m_{2}}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap jelenlegi, 2013. augusztus 27., 22:40-kori változata
Feladat
- (3.1.16) Valamely
 tömegű test rugalmatlanul ütközik egy
tömegű test rugalmatlanul ütközik egy  tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az
tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az  tömegű test az ütközés előtt nyugalomban volt!
tömegű test az ütközés előtt nyugalomban volt!
Megoldás
- Az ütközés során megmarad az impulzus és a tökéletes rugalmatlanság miatt az ütközés utáni sebességek megegyeznek. Ha az
 tömegű test ütközés előtti sebességét
tömegű test ütközés előtti sebességét 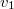 -gyel, az ütközés utáni sebességet pedig
-gyel, az ütközés utáni sebességet pedig  -vel jelöljük, akkor az impulzus megmaradást az alábbiak szerint írhatjuk fel. A kinetikus energia veszteség aránya
-vel jelöljük, akkor az impulzus megmaradást az alábbiak szerint írhatjuk fel. A kinetikus energia veszteség aránya![\[m_{1}v_{1}=(m_{1}+m_{2})v\qquad\Rightarrow\qquad v=\frac{m_{1}}{m_{1}+m_{2}}v_{1}\]](/images/math/1/c/4/1c4d9898b282950093079eabfee1eb9f.png)
![\[\frac{E_{kin,0}-E_{kin}}{E_{kin,0}}=\frac{\frac{1}{2}m_{1}v_{1}^{2}-\frac{1}{2}(m_{1}+m_{2})v^{2}}{\frac{1}{2}m_{1}v_{1}^{2}}=\frac{m_{2}}{m_{1}+m_{2}}\,.\]](/images/math/4/a/c/4acbbef7f6072086b353b70de4ca1e90.png)
- Az ütközés során megmarad az impulzus és a tökéletes rugalmatlanság miatt az ütközés utáni sebességek megegyeznek. Ha az