„Mechanika - Kritikus csillapítás” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (6.31.) Hogyan változik meg az előző feladatban a test mozgása, ha olyan rugóra akasztjuk, amely $1\,\rm N$ hatására $8\,\rm{cm}$-rel nyúlik meg és minden egyéb körülményt változatlanul hagyunk?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$x(t)=e^{-5t}(0,05+0, | + | </noinclude><wlatex># (6.31.) Hogyan változik meg az előző feladatban a test mozgása, ha olyan rugóra akasztjuk, amely $1\,\rm N$ hatására $8\,\rm{cm}$-rel nyúlik meg és minden egyéb körülményt változatlanul hagyunk?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$x(t)=e^{-5t}(0,05+0,25t),$$ ahol a számértékek SI alapegységekben értendők.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>Mivel a rugóerő tízszeresére változott $D=12,5\,\rm{\frac Nm}$, $\omega_0=\sqrt{25}\,\frac1{\rm s}=5\,\frac1{\rm s}$, amely épp megegyezik a $\beta$ csillapítási tényezővel, így a rezgés kritikusan csillapított. Az ehhez tartozó általános megoldás $$x(t)=e^{-\beta t}(c_1+c_2t)$$ A kezdeti feltételek illesztése: $$x(0)=1(c_1+c_20)=c_1=5\,\rm{cm}$$ $$\dot x(t)=-\beta e^{-\beta t}(c_1+c_2t)+e^{-\beta t}c_2$$ $$\dot x(0)=-\beta c_1+c_2=0$$ $$c_2=\beta c_1$$</wlatex> | + | <wlatex>Mivel a rugóerő tízszeresére változott $D=12,5\,\rm{\frac Nm}$, $\omega_0=\sqrt{25}\,\frac1{\rm s}=5\,\frac1{\rm s}$, amely épp megegyezik a $\beta$ csillapítási tényezővel, így a rezgés kritikusan csillapított. Az ehhez tartozó általános megoldás $$x(t)=e^{-\beta t}(c_1+c_2t)$$ A kezdeti feltételek illesztése: $$x(0)=1(c_1+c_20)=c_1=5\,\rm{cm}$$ $$\dot x(t)=-\beta e^{-\beta t}(c_1+c_2t)+e^{-\beta t}c_2$$ $$\dot x(0)=-\beta c_1+c_2=0$$ $$c_2=\beta c_1=0,25\,\rm{m/s}$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 29., 14:27-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (6.31.) Hogyan változik meg az előző feladatban a test mozgása, ha olyan rugóra akasztjuk, amely
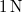hatására 
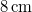-rel nyúlik meg és minden egyéb körülményt változatlanul hagyunk?
Megoldás
Mivel a rugóerő tízszeresére változott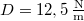
, 
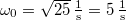, amely épp megegyezik a 
csillapítási tényezővel, így a rezgés kritikusan csillapított. Az ehhez tartozó általános megoldás ![\[x(t)=e^{-\beta t}(c_1+c_2t)\]](/images/math/1/9/c/19c79b90e51713c430edff8a68b8add9.png)
![\[x(0)=1(c_1+c_20)=c_1=5\,\rm{cm}\]](/images/math/9/c/9/9c900ebc8162e0a8a6ff0e8a340290a0.png)
![\[\dot x(t)=-\beta e^{-\beta t}(c_1+c_2t)+e^{-\beta t}c_2\]](/images/math/a/1/9/a1982860acad4c1009cc050f99e4e2f3.png)
![\[\dot x(0)=-\beta c_1+c_2=0\]](/images/math/1/d/b/1dbc8fcc38280835a39c11cf39d374a2.png)
![\[c_2=\beta c_1=0,25\,\rm{m/s}\]](/images/math/5/d/5/5d5cda6e306487ade0d119bf060527ef.png)
