„Pontrendszerek - 3.1.26” változatai közötti eltérés
A Fizipedia wikiből
a (→Feladat) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (3.1.26) A rakétát a hajtóműből folytonosan kiáramló gáz gyorsítja. Mennyivel változik az eredetileg $m_{0}$ tömegű rakéta sebessége, ha a rakétából a rakétához viszonyítva állandó $u$ sebességgel $\alpha m_{0}$ tömegű gáz áramlott ki, ahol $0<\alpha<1$? (A rakétára külső erő nem hat és az $u$ sebesség a rakéta sebességével ellentétes irányú, de azzal egy egyenesbe esik.) | + | </noinclude><wlatex># (*3.1.26) A rakétát a hajtóműből folytonosan kiáramló gáz gyorsítja. Mennyivel változik az eredetileg $m_{0}$ tömegű rakéta sebessége, ha a rakétából a rakétához viszonyítva állandó $u$ sebességgel $\alpha m_{0}$ tömegű gáz áramlott ki, ahol $0<\alpha<1$? (A rakétára külső erő nem hat és az $u$ sebesség a rakéta sebességével ellentétes irányú, de azzal egy egyenesbe esik.) |
</wlatex><includeonly><wlatex>{{Útmutatás|content= Vizsgálja egy általános időpillanatban egy $dm$ infinitezimális tömegű gázmennyiség kilökődését!}}{{Végeredmény|content=$$\Delta v_{\alpha}=-u\ln(1-\alpha)>0$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content= Vizsgálja egy általános időpillanatban egy $dm$ infinitezimális tömegű gázmennyiség kilökődését!}}{{Végeredmény|content=$$\Delta v_{\alpha}=-u\ln(1-\alpha)>0$$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>#: A gáz kiáramlását jellemezze a konstans $\lambda$ kiáramlási sebesség. Egy nagyon rövid $dt$ időtartam alatt így $dm=\lambda dt$ tömegű gáz áramlik ki. Ezen idő alatt tekinthetünk úgy a problémára, mintha a rakéta két részre szakadna. A ''szétszakadás'' előtt a teljes tömeg $m(t)$, utána a kilökött gázé $dm=\lambda dt$, a rakétáé pedig $m(t+dt)=m(t)-\lambda dt$. A rakéta sebessége a ''szétszakadás'' előtt $v(t)$, utána a kilökött gázé $v(t)-u$, a rakétáé $v(t+dt)$. Az impulzus megmaradás az alábbiak szerint írható fel. $$m(t)v(t)=(m(t)-\lambda dt)v(t+dt)+\lambda dt(v(t)-u)$$ Infinitezimális folyamatokat írunk le, ezért $dt$ nagyon kicsi. Így mindkét oldalon csak $dt$-ben elsőrendű tagokat tartjuk meg. $$m(t)v(t)=m(t)v(t+dt)-\lambda dt u$$ Az elhanyagolt tag $\sim (v(t+dt)-v(t))dt=a(t) dt^{2}$ nagyságrendű. Az így kapott egyenletet leosztva $dt$-vel megjelenik a sebesség idő szerinti deriváltja. $$m(t)\frac{dv}{dt}=\lambda u\,,$$ ahol $m(t)=m_{0}-\lambda t$. $$\frac{dv}{dt}=\frac{\lambda u}{m_{0}-\lambda t}\qquad\Rightarrow\qquad v(t)=v(0)+\int_{0}^{t}\frac{\lambda u}{m_{0}-\lambda t'}dt'=v(0)+u\ln\frac{m_{0}}{m_{0}-\lambda t}$$ A $t_{\alpha}=\alpha m_{0}/\lambda$ az az idő, amennyi alatt az $\alpha m_{0}$ mennyiségű gáz kiáramlik. Ennyi idő alatt a sebesség változás $$\Delta v_{\alpha}=v(t_{\alpha})-v(0)=-u\ln(1-\alpha)>0\,.$$ | <wlatex>#: A gáz kiáramlását jellemezze a konstans $\lambda$ kiáramlási sebesség. Egy nagyon rövid $dt$ időtartam alatt így $dm=\lambda dt$ tömegű gáz áramlik ki. Ezen idő alatt tekinthetünk úgy a problémára, mintha a rakéta két részre szakadna. A ''szétszakadás'' előtt a teljes tömeg $m(t)$, utána a kilökött gázé $dm=\lambda dt$, a rakétáé pedig $m(t+dt)=m(t)-\lambda dt$. A rakéta sebessége a ''szétszakadás'' előtt $v(t)$, utána a kilökött gázé $v(t)-u$, a rakétáé $v(t+dt)$. Az impulzus megmaradás az alábbiak szerint írható fel. $$m(t)v(t)=(m(t)-\lambda dt)v(t+dt)+\lambda dt(v(t)-u)$$ Infinitezimális folyamatokat írunk le, ezért $dt$ nagyon kicsi. Így mindkét oldalon csak $dt$-ben elsőrendű tagokat tartjuk meg. $$m(t)v(t)=m(t)v(t+dt)-\lambda dt u$$ Az elhanyagolt tag $\sim (v(t+dt)-v(t))dt=a(t) dt^{2}$ nagyságrendű. Az így kapott egyenletet leosztva $dt$-vel megjelenik a sebesség idő szerinti deriváltja. $$m(t)\frac{dv}{dt}=\lambda u\,,$$ ahol $m(t)=m_{0}-\lambda t$. $$\frac{dv}{dt}=\frac{\lambda u}{m_{0}-\lambda t}\qquad\Rightarrow\qquad v(t)=v(0)+\int_{0}^{t}\frac{\lambda u}{m_{0}-\lambda t'}dt'=v(0)+u\ln\frac{m_{0}}{m_{0}-\lambda t}$$ A $t_{\alpha}=\alpha m_{0}/\lambda$ az az idő, amennyi alatt az $\alpha m_{0}$ mennyiségű gáz kiáramlik. Ennyi idő alatt a sebesség változás $$\Delta v_{\alpha}=v(t_{\alpha})-v(0)=-u\ln(1-\alpha)>0\,.$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 9., 16:40-kori változata
Feladat
- (*3.1.26) A rakétát a hajtóműből folytonosan kiáramló gáz gyorsítja. Mennyivel változik az eredetileg
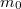 tömegű rakéta sebessége, ha a rakétából a rakétához viszonyítva állandó
tömegű rakéta sebessége, ha a rakétából a rakétához viszonyítva állandó 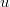 sebességgel
sebességgel 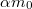 tömegű gáz áramlott ki, ahol
tömegű gáz áramlott ki, ahol 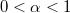 ? (A rakétára külső erő nem hat és az
? (A rakétára külső erő nem hat és az 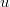 sebesség a rakéta sebességével ellentétes irányú, de azzal egy egyenesbe esik.)
sebesség a rakéta sebességével ellentétes irányú, de azzal egy egyenesbe esik.)
Megoldás
- A gáz kiáramlását jellemezze a konstans
 kiáramlási sebesség. Egy nagyon rövid
kiáramlási sebesség. Egy nagyon rövid 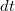 időtartam alatt így
időtartam alatt így 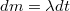 tömegű gáz áramlik ki. Ezen idő alatt tekinthetünk úgy a problémára, mintha a rakéta két részre szakadna. A szétszakadás előtt a teljes tömeg
tömegű gáz áramlik ki. Ezen idő alatt tekinthetünk úgy a problémára, mintha a rakéta két részre szakadna. A szétszakadás előtt a teljes tömeg 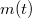 , utána a kilökött gázé
, utána a kilökött gázé 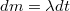 , a rakétáé pedig
, a rakétáé pedig 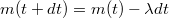 . A rakéta sebessége a szétszakadás előtt
. A rakéta sebessége a szétszakadás előtt 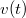 , utána a kilökött gázé
, utána a kilökött gázé 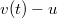 , a rakétáé
, a rakétáé 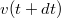 . Az impulzus megmaradás az alábbiak szerint írható fel. Infinitezimális folyamatokat írunk le, ezért
. Az impulzus megmaradás az alábbiak szerint írható fel. Infinitezimális folyamatokat írunk le, ezért![\[m(t)v(t)=(m(t)-\lambda dt)v(t+dt)+\lambda dt(v(t)-u)\]](/images/math/5/0/f/50fbaa87d92767859f2e48cbdad12649.png)
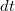 nagyon kicsi. Így mindkét oldalon csak
nagyon kicsi. Így mindkét oldalon csak 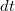 -ben elsőrendű tagokat tartjuk meg. Az elhanyagolt tag
-ben elsőrendű tagokat tartjuk meg. Az elhanyagolt tag![\[m(t)v(t)=m(t)v(t+dt)-\lambda dt u\]](/images/math/b/8/8/b88d792b5b5f4d4900a6103a06951f99.png)
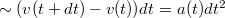 nagyságrendű. Az így kapott egyenletet leosztva
nagyságrendű. Az így kapott egyenletet leosztva 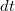 -vel megjelenik a sebesség idő szerinti deriváltja. ahol
-vel megjelenik a sebesség idő szerinti deriváltja. ahol![\[m(t)\frac{dv}{dt}=\lambda u\,,\]](/images/math/3/5/b/35b60e9b426b780a8019fe04fe270ebf.png)
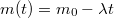 . A
. A![\[\frac{dv}{dt}=\frac{\lambda u}{m_{0}-\lambda t}\qquad\Rightarrow\qquad v(t)=v(0)+\int_{0}^{t}\frac{\lambda u}{m_{0}-\lambda t'}dt'=v(0)+u\ln\frac{m_{0}}{m_{0}-\lambda t}\]](/images/math/d/0/8/d082680bb5a029aedc3704f2804fae78.png)
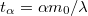 az az idő, amennyi alatt az
az az idő, amennyi alatt az 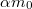 mennyiségű gáz kiáramlik. Ennyi idő alatt a sebesség változás
mennyiségű gáz kiáramlik. Ennyi idő alatt a sebesség változás ![\[\Delta v_{\alpha}=v(t_{\alpha})-v(0)=-u\ln(1-\alpha)>0\,.\]](/images/math/f/5/d/f5d3dbe371f871f3b6b6e3457330157f.png)
- A gáz kiáramlását jellemezze a konstans