„Mechanika - Pontrendszerek” változatai közötti eltérés
A Fizipedia wikiből
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 19. sor: | 19. sor: | ||
{{:Pontrendszerek - 3.1.16}}{{Megoldás|link=Pontrendszerek - 3.1.16}} | {{:Pontrendszerek - 3.1.16}}{{Megoldás|link=Pontrendszerek - 3.1.16}} | ||
{{:Pontrendszerek - 3.1.18}}{{Megoldás|link=Pontrendszerek - 3.1.18}} | {{:Pontrendszerek - 3.1.18}}{{Megoldás|link=Pontrendszerek - 3.1.18}} | ||
| + | {{:Pontrendszerek - Rugalmas ütközés térben}}{{Megoldás|link=Pontrendszerek - Rugalmas ütközés térben}} | ||
{{:Pontrendszerek - 3.1.21}}{{Megoldás|link=Pontrendszerek - 3.1.21}} | {{:Pontrendszerek - 3.1.21}}{{Megoldás|link=Pontrendszerek - 3.1.21}} | ||
{{:Pontrendszerek - 3.1.23}}{{Megoldás|link=Pontrendszerek - 3.1.23}} | {{:Pontrendszerek - 3.1.23}}{{Megoldás|link=Pontrendszerek - 3.1.23}} | ||
{{:Pontrendszerek - 3.1.26}}{{Megoldás|link=Pontrendszerek - 3.1.26}} | {{:Pontrendszerek - 3.1.26}}{{Megoldás|link=Pontrendszerek - 3.1.26}} | ||
{{:Pontrendszerek - 3.3.1}}{{Megoldás|link=Pontrendszerek - 3.3.1}} | {{:Pontrendszerek - 3.3.1}}{{Megoldás|link=Pontrendszerek - 3.3.1}} | ||
| − | |||
A lap jelenlegi, 2014. október 21., 15:14-kori változata
Feladatok
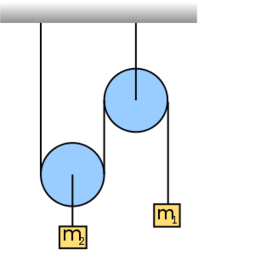
- (3.1.2) Egy súrlódásmentes álló csigán átvetett fonálon egy
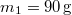 és egy
és egy 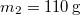 tömegű test függ. A nehezebb test a földfelszín felett
tömegű test függ. A nehezebb test a földfelszín felett 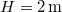 -re van. Magára hagyva a rendszert, mennyi idő alatt ér le a nagyobb tömegű test a talajra? Feltesszük, hogy a fonál elegendően hosszú. A csiga és a fonál tömegét elhanyagolhatjuk.
-re van. Magára hagyva a rendszert, mennyi idő alatt ér le a nagyobb tömegű test a talajra? Feltesszük, hogy a fonál elegendően hosszú. A csiga és a fonál tömegét elhanyagolhatjuk.
- (*3.1.3) Egy mozgó csigára egy
 tömegű testet függesztünk. A mozgó csigát tartó fonál egyik végét állványhoz erősítjük, másik végét álló csigán átvezetve
tömegű testet függesztünk. A mozgó csigát tartó fonál egyik végét állványhoz erősítjük, másik végét álló csigán átvezetve  tömeghez kötjük. Határozzuk meg az
tömeghez kötjük. Határozzuk meg az  , ill.
, ill.  tömegek gyorsulását! A csigák és a fonál tömegétől, valamint a súrlódástól eltekintünk.
tömegek gyorsulását! A csigák és a fonál tömegétől, valamint a súrlódástól eltekintünk.
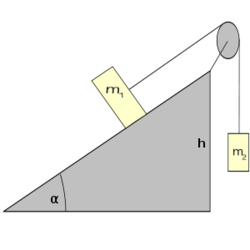
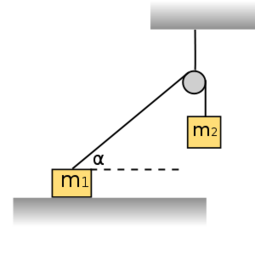
- (3.1.6) Egy
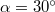 hajlásszögű lejtőre helyezett
hajlásszögű lejtőre helyezett 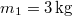 tömegű testhez a lejtő tetején megerősített csigán átvetett fonállal
tömegű testhez a lejtő tetején megerősített csigán átvetett fonállal 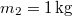 tömegű testet kötünk. (3.1.6. ábra) Határozzuk meg a rendszer gyorsulását, valamint a fonalat feszítő erőt! Mekkora sebességet ér el a
tömegű testet kötünk. (3.1.6. ábra) Határozzuk meg a rendszer gyorsulását, valamint a fonalat feszítő erőt! Mekkora sebességet ér el a 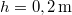 magasságú lejtő tetejéről kezdősebesség nélkül induló test a lejtő alján? A csiga és a fonál tömegétől, valamint a súrlódástól eltekintünk.
magasságú lejtő tetejéről kezdősebesség nélkül induló test a lejtő alján? A csiga és a fonál tömegétől, valamint a súrlódástól eltekintünk.
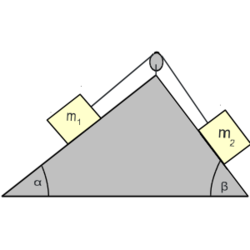
- (3.1.7) Kétoldalú lejtő felső pontjában rögzített csigán átvetett fonál egyik végéhez kötött
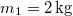 tömegű test az
tömegű test az 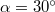 , másik végéhez kötött
, másik végéhez kötött 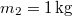 tömegű test a
tömegű test a 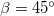 hajlásszögű lejtőn fekszik. Határozzuk meg a gyorsulást és a fonalat feszítő erőt, ha a súrlódástól és a csiga tömegétől eltekintünk!
hajlásszögű lejtőn fekszik. Határozzuk meg a gyorsulást és a fonalat feszítő erőt, ha a súrlódástól és a csiga tömegétől eltekintünk!
- (*3.1.9) Vízszintes talajon
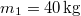 tömegű láda fekszik, a súrlódási együttható
tömegű láda fekszik, a súrlódási együttható 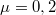 . Mekkora
. Mekkora  tömegű test képes a ládát megmozdítani az ábrán látható elrendezésben? Mekkora pillanatnyi gyorsulással indulna el ilyen
tömegű test képes a ládát megmozdítani az ábrán látható elrendezésben? Mekkora pillanatnyi gyorsulással indulna el ilyen  tömeg hatására a láda egy súrlódásmentes vízszintes síkon? A csiga tömegét és súrlódását a számításokban elhanyagolhatjuk. (
tömeg hatására a láda egy súrlódásmentes vízszintes síkon? A csiga tömegét és súrlódását a számításokban elhanyagolhatjuk. (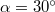 )
)
- (3.1.11) Az
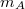 tömegű
tömegű  és az
és az 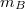 tömegű
tömegű  szabad anyagi pontok Newton törvénye szerint kölcsönösen vonzzák egymást. A kezdő időpontban az
szabad anyagi pontok Newton törvénye szerint kölcsönösen vonzzák egymást. A kezdő időpontban az  pont sebessége
pont sebessége 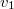 és
és 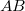 -re merőleges,
-re merőleges,  pont sebessége
pont sebessége 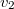 ,
, 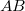 irányú és
irányú és  -tól elfelé mutat. Határozzuk meg a pontok súlypontjának pályáját és sebességét!
-tól elfelé mutat. Határozzuk meg a pontok súlypontjának pályáját és sebességét!
- (3.1.12) Egy
 hosszúságú
hosszúságú  tömegű, a vízhez képest nyugvó csónak egyik végén
tömegű, a vízhez képest nyugvó csónak egyik végén  tömegű ember áll, majd átmegy a csónak másik végébe. Elhanyagolva a víz ellenállását számítsuk ki, hogy mennyit mozdul el ezalatt a csónak!
tömegű ember áll, majd átmegy a csónak másik végébe. Elhanyagolva a víz ellenállását számítsuk ki, hogy mennyit mozdul el ezalatt a csónak!
- (3.1.13) Egy
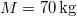 tömegű ember kezében
tömegű ember kezében 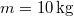 tömegű teherrel a vízszintessel
tömegű teherrel a vízszintessel 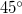 -os szöget bezáró irányban
-os szöget bezáró irányban 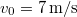 kezdősebességgel felugrik. Pályája tetőpontján a terhet vízszintes
kezdősebességgel felugrik. Pályája tetőpontján a terhet vízszintes 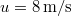 relatív sebességgel hátrafelé hajítja. Mennyivel nagyobb távolságra ugrik ily módon?
relatív sebességgel hátrafelé hajítja. Mennyivel nagyobb távolságra ugrik ily módon?
- (*3.1.14) Egy súrlódásmentes asztalon
 hajlásszögű,
hajlásszögű,  tömegű lejtő van, amelynek alapja
tömegű lejtő van, amelynek alapja  hosszú. A lejtő tetején egy
hosszú. A lejtő tetején egy  tömegű test van. Mekkora távolságra mozdul el a lejtő azalatt míg a test a lejtő aljára csúszik le?
tömegű test van. Mekkora távolságra mozdul el a lejtő azalatt míg a test a lejtő aljára csúszik le?
- (3.1.16) Valamely
 tömegű test rugalmatlanul ütközik egy
tömegű test rugalmatlanul ütközik egy  tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az
tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az  tömegű test az ütközés előtt nyugalomban volt!
tömegű test az ütközés előtt nyugalomban volt!
- (3.1.18) Két rugalmas golyó ugyanakkora
 nagyságú sebességgel halad egymás felé vízszintes egyenesen. Tökéletesen rugalmas ütközés után az egyik golyó nyugalomban marad. Mekkora lesz a másik golyó ütközés előtti és utáni
nagyságú sebességgel halad egymás felé vízszintes egyenesen. Tökéletesen rugalmas ütközés után az egyik golyó nyugalomban marad. Mekkora lesz a másik golyó ütközés előtti és utáni 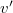 sebességeinek aránya? Mekkora a golyók tömegeinek aránya?
sebességeinek aránya? Mekkora a golyók tömegeinek aránya?
- Egy
 tömegű részecske vele azonos tömegű, álló részecskének ütközik, rugalmasan. Mutassuk meg, hogy a két részecske ütközés utáni sebességvektorai merőlegesek egymásra!
tömegű részecske vele azonos tömegű, álló részecskének ütközik, rugalmasan. Mutassuk meg, hogy a két részecske ütközés utáni sebességvektorai merőlegesek egymásra!
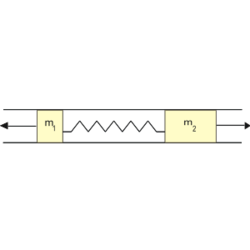
- (3.1.21) Egy összenyomott rugó hirtelen szétlök két henger alakú tömeget egymással ellentétes irányban. A tömegek nagysága
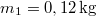 és
és 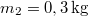 . Mekkora sebességgel haladnak ezek a vázolt csőben, ha az összenyomott rugó helyzeti energiája
. Mekkora sebességgel haladnak ezek a vázolt csőben, ha az összenyomott rugó helyzeti energiája 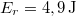 volt? Hogyan módosul az eredmény, ha az
volt? Hogyan módosul az eredmény, ha az  vagy az
vagy az  tömegű testet a csőben rögzítjük?
tömegű testet a csőben rögzítjük?
- (*3.1.23) Egy fonal egyik végét a mennyezethez erősítjük, másik végére
 tömegű testet akasztunk, ehhez egy rugót kötünk, majd a rugóra egy
tömegű testet akasztunk, ehhez egy rugót kötünk, majd a rugóra egy  tömegű testet. Kezdetben a rendszer nyugalomban van. Ekkor elégetjük a fonalat. Mekkora lesz a testek gyorsulása a következő pillanatban?
tömegű testet. Kezdetben a rendszer nyugalomban van. Ekkor elégetjük a fonalat. Mekkora lesz a testek gyorsulása a következő pillanatban?
- (*3.1.26) A rakétát a hajtóműből folytonosan kiáramló gáz gyorsítja. Mennyivel változik az eredetileg
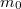 tömegű rakéta sebessége, ha a rakétából a rakétához viszonyítva állandó
tömegű rakéta sebessége, ha a rakétából a rakétához viszonyítva állandó 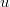 sebességgel
sebességgel 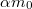 tömegű gáz áramlott ki, ahol
tömegű gáz áramlott ki, ahol 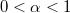 ? (A rakétára külső erő nem hat és az
? (A rakétára külső erő nem hat és az 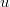 sebesség a rakéta sebességével ellentétes irányú, de azzal egy egyenesbe esik.)
sebesség a rakéta sebességével ellentétes irányú, de azzal egy egyenesbe esik.)
- (3.3.1) Lövedékek sebességének mérésére az ún. ballisztikus ingát használják. A homokkal töltött
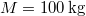 tömegű inga
tömegű inga 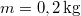 -os lövedék becsapódása után
-os lövedék becsapódása után 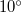 -kal kilendül. Mekkora a lövedék sebessége? Az inga súlypontjának a felfüggesztési ponttól való távolsága
-kal kilendül. Mekkora a lövedék sebessége? Az inga súlypontjának a felfüggesztési ponttól való távolsága 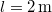 .
.
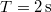
![\[a=\frac{4m_{1}-2m_{2}}{4m_{1}+m_{2}}g\]](/images/math/4/f/b/4fb9cc29689b916ebde4c928e5c10524.png)

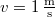

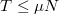 szerint adhatjuk meg.
szerint adhatjuk meg. 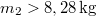
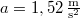
![\[\mathbf{v}_{TKP}=\frac{1}{m_{A}+m_{B}}\left[\begin{array}{c} m_{A}v_{1} \\ m_{B}v_{2}\end{array}\right]\]](/images/math/e/3/3/e33e566dfd02730dabafa9078e26e409.png)
![\[x=\frac{m}{m+M}l\]](/images/math/9/9/d/99d0b86206d9a56044a7a45e826337c7.png)
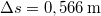
![\[d=\frac{m}{m+M}l\]](/images/math/7/9/3/79347b10fe7ff34d47474eda1e446f78.png)
![\[\frac{E_{kin,0}-E_{kin}}{E_{kin,0}}=\frac{m_{2}}{m_{1}+m_{2}}\]](/images/math/c/8/4/c848912cb98b0f8574daa3cbab813564.png)
![\[m_{1}=3m_{2}\qquad\qquad \frac{v'}{v}=2\,.\]](/images/math/0/4/4/0443359e063bd9894b25af280f9dfd7b.png)
![\[v_{1}=12,78\,\mathrm{\frac{m}{s}} \qquad\qquad v_{2}=5,11\,\mathrm{\frac{m}{s}}\]](/images/math/3/9/e/39e63f97e5ba423b61366df672ff4287.png)
![\[v_{1}'=9,04\,\mathrm{\frac{m}{s}}\]](/images/math/3/4/4/344005f749a4db88dd192099acf54a2d.png)
![\[v_{2}'=5,76\,\mathrm{\frac{m}{s}}\]](/images/math/a/2/1/a211bfe03172f5eb39c95e203dc47160.png)

![\[a_{1}=g\left(1+\frac{m_{2}}{m_{1}}\right)\qquad\qquad a_{2}=0\]](/images/math/3/d/e/3decb84b1fbb4b09dd59d6855d8eb957.png)
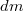 infinitezimális tömegű gázmennyiség kilökődését!
infinitezimális tömegű gázmennyiség kilökődését! ![\[\Delta v_{\alpha}=-u\ln(1-\alpha)>0\]](/images/math/4/e/2/4e24d5be4488ca7a258fff53e5725d40.png)