„Mechanika - Forgó lemez közegellenállással” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 12. sor: | 12. sor: | ||
#: b) Mekkora a lemezre ható nyomaték nagysága? | #: b) Mekkora a lemezre ható nyomaték nagysága? | ||
#: c) Hogyan változik a lemez szöggyorsulása és szögsebessége az idő függvényében? | #: c) Hogyan változik a lemez szöggyorsulása és szögsebessége az idő függvényében? | ||
| − | #: d) Mekkora és hol van a támadáspontja az eredő közegellenállási erőnek?</wlatex><includeonly><wlatex>{{Útmutatás|content=Mind az eredő erőt mind az eredő forgatónyomatékot a megfelelő erő- és nyomatékelemek felületre vett integráljával lehet meghatározni Az eredő nyomaték az eredő erő és a támadáspont sugarának szorzata.}}{{Végeredmény|content=$$M=bk\omega^2(t)\frac{a^4}4$$ $$\omega(t)=\frac{\omega_0}{1-\frac{a^4\omega_0bkt}{4\theta}}$$ A szöggyorsulás ebből deriválással megkapható.}}</wlatex></includeonly><noinclude> | + | #: d) Mekkora és hol van a támadáspontja az eredő közegellenállási erőnek?</wlatex><includeonly><wlatex>{{Útmutatás|content=Mind az eredő erőt mind az eredő forgatónyomatékot a megfelelő erő- és nyomatékelemek felületre vett integráljával lehet meghatározni Az eredő nyomaték az eredő erő és a támadáspont sugarának szorzata.}}{{Végeredmény|content=$$M=bk\omega^2(t)\frac{a^4}4$$ $$\omega(t)=\frac{\omega_0}{1-\frac{a^4\omega_0bkt}{4\theta}}$$ A szöggyorsulás ebből deriválással megkapható. $$F=bk\omega^2a^3/3$$ $$R=\frac3 4 a$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>Az elemi felületre ható közegellenállási erő nagysága $$\text{d}F=kv^2(t)\text{d}A=kr^2\omega^2(t)\text{d}A$$ Mivel hengerkoordinátákban felírva $\text{d}A=\text{d}r\text{d}z$, és a közegellenállási erőelemek minden pontban merőlegesek a lapra, $$\text{d}M=\text{d}F\cdot r,$$ így a teljes forgatónyomaték $$M=\int\int \text{d}M=\int_0^b\int_0^a rkr^2\omega^2\text{d}r\text{d}z=bk\omega^2\int_0^a r^3\rm{d}r=bk\omega^2(t)\frac{a^4}4$$ Ezzel a lemez mozgásegyenlete $$bk\frac{a^4}4\omega^2(t)=\theta\beta(t)=\theta\frac{d\omega(t)}{dt},$$ amely szeparálható $$\frac{a^4bk}{4\theta}dt=\frac{d\omega}{\omega^2}$$ alakba, ezt integrálva $\tilde t=0$-tól $t$-ig kapjuk a következőt: $$\frac{a^4bkt}{4\theta}=\left[-\frac1{\tilde{\omega}^2}\right]_{\omega_0}^{\omega}=\frac1\omega_0-\frac1\omega,$$ ebből $$\frac1\omega=\frac1\omega_0-\frac{a^4bkt}{4\theta}$$ végül $$\omega(t)=\frac1{\frac1\omega_0-\frac{a^4bkt}{4\theta}}=\frac{\omega_0}{1-\frac{a^4\omega_0bkt}{4\theta}}$$ Mivel láthatóan $b$ értéke tetszőleges $a$-hoz képest, $b<<a$absztrakcióval belátható, hogy a lap tehetetlenségé nyomatéka megegyezik egy $a$ hosszúságú, végpontja körül forgatott rúdéval, tehát $\theta=\frac13ma^2$. A fenti megoldásban a közegellenállás fékező hatását az biztosítja, ha $k<0$, ekkor a nevező mindig pozitív, és $\omega$ az idő függvényében csökken $\omega_0$-ról indulva. $\omega(t)$ függvényből a szöggyorsulás időfüggése (amely mindvégig negatív) további idő szerinti deriválással megkapható.</wlatex> | + | <wlatex>Az elemi felületre ható közegellenállási erő nagysága $$\text{d}F=kv^2(t)\text{d}A=kr^2\omega^2(t)\text{d}A$$ Mivel hengerkoordinátákban felírva $\text{d}A=\text{d}r\text{d}z$, és a közegellenállási erőelemek minden pontban merőlegesek a lapra, $$\text{d}M=\text{d}F\cdot r,$$ így a teljes forgatónyomaték $$M=\int\int \text{d}M=\int_0^b\int_0^a rkr^2\omega^2\text{d}r\text{d}z=bk\omega^2\int_0^a r^3\rm{d}r=bk\omega^2(t)\frac{a^4}4$$ Ezzel a lemez mozgásegyenlete $$bk\frac{a^4}4\omega^2(t)=\theta\beta(t)=\theta\frac{d\omega(t)}{dt},$$ amely szeparálható $$\frac{a^4bk}{4\theta}dt=\frac{d\omega}{\omega^2}$$ alakba, ezt integrálva $\tilde t=0$-tól $t$-ig kapjuk a következőt: $$\frac{a^4bkt}{4\theta}=\left[-\frac1{\tilde{\omega}^2}\right]_{\omega_0}^{\omega}=\frac1\omega_0-\frac1\omega,$$ ebből $$\frac1\omega=\frac1\omega_0-\frac{a^4bkt}{4\theta}$$ végül $$\omega(t)=\frac1{\frac1\omega_0-\frac{a^4bkt}{4\theta}}=\frac{\omega_0}{1-\frac{a^4\omega_0bkt}{4\theta}}$$ Mivel láthatóan $b$ értéke tetszőleges $a$-hoz képest, $b<<a$absztrakcióval belátható, hogy a lap tehetetlenségé nyomatéka megegyezik egy $a$ hosszúságú, végpontja körül forgatott rúdéval, tehát $\theta=\frac13ma^2$. A fenti megoldásban a közegellenállás fékező hatását az biztosítja, ha $k<0$, ekkor a nevező mindig pozitív, és $\omega$ az idő függvényében csökken $\omega_0$-ról indulva. $\omega(t)$ függvényből a szöggyorsulás időfüggése (amely mindvégig negatív) további idő szerinti deriválással megkapható. Az eredő erő $$F=bk\omega^2a^3/3$$ és a támadáspont $$R=\frac MF=\frac3 4 a$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2012. november 8., 15:44-kori változata
Feladat
- (**3.2.10.) Egy
 és
és  oldalhosszúságú
oldalhosszúságú  tömegű téglalap alakú lemez függőlegesen elhelyezkedő
tömegű téglalap alakú lemez függőlegesen elhelyezkedő  oldala mentén levő tengely körül forog. A
oldala mentén levő tengely körül forog. A  időpontban szögsebessége
időpontban szögsebessége  . A lemez felületére a közegellenállás folytán erő hat, mely a mozgását akadályozza. Egy felületelemre ható erő arányos a felületelem sebességének négyzetével és a felületelem nagyságával, az arányossági tényező
. A lemez felületére a közegellenállás folytán erő hat, mely a mozgását akadályozza. Egy felületelemre ható erő arányos a felületelem sebességének négyzetével és a felületelem nagyságával, az arányossági tényező  .
.
- a) Mekkora a
 -ik időpillanatban a tengelytől
-ik időpillanatban a tengelytől  távolságban elhelyezkedő
távolságban elhelyezkedő 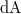 felületelemre ható, közegellenállásból származó erő?
felületelemre ható, közegellenállásból származó erő?
- b) Mekkora a lemezre ható nyomaték nagysága?
- c) Hogyan változik a lemez szöggyorsulása és szögsebessége az idő függvényében?
- d) Mekkora és hol van a támadáspontja az eredő közegellenállási erőnek?
- a) Mekkora a
Megoldás
Az elemi felületre ható közegellenállási erő nagysága![\[\text{d}F=kv^2(t)\text{d}A=kr^2\omega^2(t)\text{d}A\]](/images/math/5/b/5/5b51a2bc13463c18706e570498ddfc63.png)
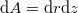 , és a közegellenállási erőelemek minden pontban merőlegesek a lapra,
, és a közegellenállási erőelemek minden pontban merőlegesek a lapra, ![\[\text{d}M=\text{d}F\cdot r,\]](/images/math/d/5/4/d54cc02b28f3a05001a2179c5a0b12c6.png)
![\[M=\int\int \text{d}M=\int_0^b\int_0^a rkr^2\omega^2\text{d}r\text{d}z=bk\omega^2\int_0^a r^3\rm{d}r=bk\omega^2(t)\frac{a^4}4\]](/images/math/9/c/0/9c0caac20c39b404a827ce44017c40f0.png)
![\[bk\frac{a^4}4\omega^2(t)=\theta\beta(t)=\theta\frac{d\omega(t)}{dt},\]](/images/math/0/a/2/0a2dd780dec13aca10529af8b794fa2a.png)
![\[\frac{a^4bk}{4\theta}dt=\frac{d\omega}{\omega^2}\]](/images/math/c/c/b/ccb7a14cb8eca9b05cc2c397be11c511.png)
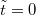 -tól
-tól  -ig kapjuk a következőt:
-ig kapjuk a következőt: ![\[\frac{a^4bkt}{4\theta}=\left[-\frac1{\tilde{\omega}^2}\right]_{\omega_0}^{\omega}=\frac1\omega_0-\frac1\omega,\]](/images/math/f/6/7/f67929e4796ebd042a126847b7e8b9da.png)
![\[\frac1\omega=\frac1\omega_0-\frac{a^4bkt}{4\theta}\]](/images/math/9/2/8/9280709774e1c41d2c36f89d80d7d602.png)
![\[\omega(t)=\frac1{\frac1\omega_0-\frac{a^4bkt}{4\theta}}=\frac{\omega_0}{1-\frac{a^4\omega_0bkt}{4\theta}}\]](/images/math/d/8/4/d845ae80b14a00c97bf0887d0adeb759.png)
 értéke tetszőleges
értéke tetszőleges  -hoz képest,
-hoz képest, 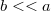 absztrakcióval belátható, hogy a lap tehetetlenségé nyomatéka megegyezik egy
absztrakcióval belátható, hogy a lap tehetetlenségé nyomatéka megegyezik egy  hosszúságú, végpontja körül forgatott rúdéval, tehát
hosszúságú, végpontja körül forgatott rúdéval, tehát 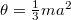 . A fenti megoldásban a közegellenállás fékező hatását az biztosítja, ha
. A fenti megoldásban a közegellenállás fékező hatását az biztosítja, ha 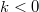 , ekkor a nevező mindig pozitív, és
, ekkor a nevező mindig pozitív, és  az idő függvényében csökken
az idő függvényében csökken  -ról indulva.
-ról indulva. 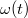 függvényből a szöggyorsulás időfüggése (amely mindvégig negatív) további idő szerinti deriválással megkapható. Az eredő erő
függvényből a szöggyorsulás időfüggése (amely mindvégig negatív) további idő szerinti deriválással megkapható. Az eredő erő ![\[F=bk\omega^2a^3/3\]](/images/math/a/9/7/a97afbfbe81ef8baabe4f30dfede92f8.png)
![\[R=\frac MF=\frac3 4 a\]](/images/math/0/f/e/0feb06faba1b88343a46997f70126d98.png)