„Mechanika - Korongba lőtt golyó” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév …”) |
a (→Feladat) |
||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
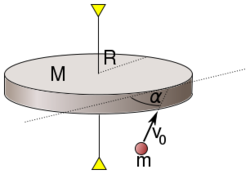
| − | </noinclude><wlatex># | + | </noinclude><wlatex># Egy $M$ tömegű, $R$ sugarú vízszintes korong a szimmetriatengelyén átmenő, függőleges tengely körül foroghat. A korong kezdetben áll. Egy $m$ tömegű golyót lövünk a korongnak vízszintesen $v_0$ sebességgel úgy, hogy a sebességvektor a korong vízszintes érintőjével $\alpha$ szöget zár be, ahogy az ábra is mutatja. A golyó és a korong tökéletesen rugalmatlanul ütközik, a golyó hozzátapad a koronghoz. |
#: a.) Mekkora lesz az ütközés után a korong szögsebessége? | #: a.) Mekkora lesz az ütközés után a korong szögsebessége? | ||
#: b.) Hányad része vész el a kezdeti mozgási energiának? | #: b.) Hányad része vész el a kezdeti mozgási energiának? | ||
A lap jelenlegi, 2014. október 28., 12:42-kori változata
Feladat
- Egy
tömegű, 
sugarú vízszintes korong a szimmetriatengelyén átmenő, függőleges tengely körül foroghat. A korong kezdetben áll. Egy 
tömegű golyót lövünk a korongnak vízszintesen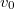 
sebességgel úgy, hogy a sebességvektor a korong vízszintes érintőjével 
szöget zár be, ahogy az ábra is mutatja. A golyó és a korong tökéletesen rugalmatlanul ütközik, a golyó hozzátapad a koronghoz.
- a.) Mekkora lesz az ütközés után a korong szögsebessége?
- b.) Hányad része vész el a kezdeti mozgási energiának?
- c.) Legalább mekkora a golyó és korong közötti "ragasztó" erő?
Megoldás
Majd lesz
