„Mechanika - Oldalra húzott rúd egyensúlya” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># 3.2.13. Egy homogén rúd tömege $m$. Egyik végén átmenő vízszintes tengely körül elforoghat, a másik végén $m$ tömegű teher lóg. A rudat geometriai középpontjában ható $mg$ nagyságú vízszintes erővel húzzuk. Mekkora a rúd függőlegessel alkotott szöge egyensúly esetén?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\tan{\alpha}=\frac13$$}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex># (3.2.13.) Egy homogén rúd tömege $m$. Egyik végén átmenő vízszintes tengely körül elforoghat, a másik végén $m$ tömegű teher lóg. A rudat geometriai középpontjában ható $mg$ nagyságú vízszintes erővel húzzuk. Mekkora a rúd függőlegessel alkotott szöge egyensúly esetén?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\tan{\alpha}=\frac13$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>A forgatónyomatékok egyensúlya $l$ hosszúságú rúdra $$mgl\sin{\alpha}+mg\frac{l}2\sin{\alpha}=mg\frac{l}2\cos{\alpha},$$ ebből $\tan{\alpha}=\frac13$.</wlatex> | <wlatex>A forgatónyomatékok egyensúlya $l$ hosszúságú rúdra $$mgl\sin{\alpha}+mg\frac{l}2\sin{\alpha}=mg\frac{l}2\cos{\alpha},$$ ebből $\tan{\alpha}=\frac13$.</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2012. november 12., 15:03-kori változata
Feladat
- (3.2.13.) Egy homogén rúd tömege
. Egyik végén átmenő vízszintes tengely körül elforoghat, a másik végén tömegű teher lóg. A rudat geometriai középpontjában ható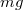 
nagyságú vízszintes erővel húzzuk. Mekkora a rúd függőlegessel alkotott szöge egyensúly esetén?
Megoldás
A forgatónyomatékok egyensúlya
hosszúságú rúdra ![\[mgl\sin{\alpha}+mg\frac{l}2\sin{\alpha}=mg\frac{l}2\cos{\alpha},\]](/images/math/6/d/0/6d05b6938dc6cc16249c278c8d5fe4b2.png)
.
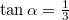