„Mechanika - Csillapodó rezgés periódusa” változatai közötti eltérés
A Fizipedia wikiből
| 10. sor: | 10. sor: | ||
</noinclude><wlatex># (*6.32.) $m=10\,\rm{kg}$ tömegű anyagi pont egy a centrumtól mért távolsággal arányos visszatérítő erő hatására egyenesvonalú lengéseket végez. A környező közeg ellenállása a pont sebességével arányos. Határozzuk meg a $T$ rezgésidőt, ha az amplitúdó három teljes lengés után tizedére csökken! (A rugóállandó: $D=20\,\rm{\frac Nm}$)</wlatex><includeonly><wlatex>{{Útmutatás|content=Vezessünk be egy időfüggő amplitúdót, és használjuk a csillapított frekvenciára vonatkozó összefüggést!}}{{Végeredmény|content=$$T=4,48\,\rm s$$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># (*6.32.) $m=10\,\rm{kg}$ tömegű anyagi pont egy a centrumtól mért távolsággal arányos visszatérítő erő hatására egyenesvonalú lengéseket végez. A környező közeg ellenállása a pont sebességével arányos. Határozzuk meg a $T$ rezgésidőt, ha az amplitúdó három teljes lengés után tizedére csökken! (A rugóállandó: $D=20\,\rm{\frac Nm}$)</wlatex><includeonly><wlatex>{{Útmutatás|content=Vezessünk be egy időfüggő amplitúdót, és használjuk a csillapított frekvenciára vonatkozó összefüggést!}}{{Végeredmény|content=$$T=4,48\,\rm s$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>Tekintsük a csillapított rezgés $x(t)=A_0e^{-\beta t}\sin(\omega t+\phi_0)$ alakját. Ha bevezetjük az $A(t)=A_0e^{-\beta t}$ időfüggő amplitúdót, akkor $A(t+3T)=\frac{A(t)}{10}$, ebből $$e^{-3\beta T}=\frac1{10},$$ amiből $$\beta T=\frac{\ln(10)}3=0,77$$ A rugóállandó és a tömeg ismeretében az $\omega_0$ csillapítatlan sajátfrekvenciát ismerjük, de sem a tényleges frekvenciát sem a csillapítási tényezőt nem, viszont a $T$ periódusidőre $$(\frac{2\pi}T)^2=\omega^2=\omega_0^2-\beta^2=\frac Dm-\beta^2$$ Ezt $T^2$-tel beszorozva $$4\pi^2=\frac{DT^2}m-(\beta T)^2,$$ amelyben már csak $T$ az ismeretlen. Rendezés után: $$T=\sqrt{\frac mD(4\pi^2+0,77^2)}=4,48\,\rm s$$</wlatex> | + | <wlatex>Tekintsük a csillapított rezgés $x(t)=A_0e^{-\beta t}\sin(\omega t+\phi_0)$ alakját. Ha bevezetjük az $A(t)=A_0e^{-\beta t}$ időfüggő amplitúdót, akkor $A(t+3T)=\frac{A(t)}{10}$, ebből $$e^{-3\beta T}=\frac1{10},$$ amiből $$\beta T=\frac{\ln(10)}3=0,77$$ A rugóállandó és a tömeg ismeretében az $\omega_0$ csillapítatlan sajátfrekvenciát ismerjük, de sem a tényleges frekvenciát sem a csillapítási tényezőt nem, viszont a $T$ periódusidőre $$\left(\frac{2\pi}T\right)^2=\omega^2=\omega_0^2-\beta^2=\frac Dm-\beta^2$$ Ezt $T^2$-tel beszorozva $$4\pi^2=\frac{DT^2}m-(\beta T)^2,$$ amelyben már csak $T$ az ismeretlen. Rendezés után: $$T=\sqrt{\frac mD(4\pi^2+0,77^2)}=4,48\,\rm s$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. április 4., 12:57-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések II. |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*6.32.)
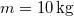 tömegű anyagi pont egy a centrumtól mért távolsággal arányos visszatérítő erő hatására egyenesvonalú lengéseket végez. A környező közeg ellenállása a pont sebességével arányos. Határozzuk meg a
tömegű anyagi pont egy a centrumtól mért távolsággal arányos visszatérítő erő hatására egyenesvonalú lengéseket végez. A környező közeg ellenállása a pont sebességével arányos. Határozzuk meg a  rezgésidőt, ha az amplitúdó három teljes lengés után tizedére csökken! (A rugóállandó:
rezgésidőt, ha az amplitúdó három teljes lengés után tizedére csökken! (A rugóállandó: 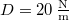 )
)
Megoldás
Tekintsük a csillapított rezgés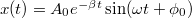 alakját. Ha bevezetjük az
alakját. Ha bevezetjük az 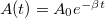 időfüggő amplitúdót, akkor
időfüggő amplitúdót, akkor 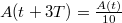 , ebből
, ebből ![\[e^{-3\beta T}=\frac1{10},\]](/images/math/8/9/6/8966a71d5ee53004116a0c8534f6f659.png)
![\[\beta T=\frac{\ln(10)}3=0,77\]](/images/math/2/b/8/2b8278ff58d7b98a1dd518860d356cc2.png)
 csillapítatlan sajátfrekvenciát ismerjük, de sem a tényleges frekvenciát sem a csillapítási tényezőt nem, viszont a
csillapítatlan sajátfrekvenciát ismerjük, de sem a tényleges frekvenciát sem a csillapítási tényezőt nem, viszont a  periódusidőre
periódusidőre ![\[\left(\frac{2\pi}T\right)^2=\omega^2=\omega_0^2-\beta^2=\frac Dm-\beta^2\]](/images/math/e/4/9/e4948fb06ac308262f0d62684e71e03d.png)
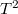 -tel beszorozva
-tel beszorozva ![\[4\pi^2=\frac{DT^2}m-(\beta T)^2,\]](/images/math/a/1/3/a13f4d52e609599abd40ad1a2e9ba583.png)
 az ismeretlen. Rendezés után:
az ismeretlen. Rendezés után: ![\[T=\sqrt{\frac mD(4\pi^2+0,77^2)}=4,48\,\rm s\]](/images/math/9/2/0/9203d4bdcad41bae537b146d50eb4c2d.png)