„Pontrendszerek - 3.1.18” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Két rugalmas golyó ugyanakkora $v$ nagyságú sebességgel halad egymás felé vízszintes egyenesen. Tökéletesen rugalmas ütközés után az egyik golyó nyugalomban marad. Mekkora lesz a másik golyó ütközés előtti és utáni $v'$ sebességeinek aránya? Mekkora a golyók tömegeinek aránya? | + | </noinclude><wlatex># (3.1.18) Két rugalmas golyó ugyanakkora $v$ nagyságú sebességgel halad egymás felé vízszintes egyenesen. Tökéletesen rugalmas ütközés után az egyik golyó nyugalomban marad. Mekkora lesz a másik golyó ütközés előtti és utáni $v'$ sebességeinek aránya? Mekkora a golyók tömegeinek aránya? |
</wlatex><includeonly><wlatex>{{Végeredmény|content=$$m_{1}=3m_{2}\qquad\qquad \frac{v'}{v}=2\,.$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$m_{1}=3m_{2}\qquad\qquad \frac{v'}{v}=2\,.$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap jelenlegi, 2013. augusztus 27., 21:40-kori változata
Feladat
- (3.1.18) Két rugalmas golyó ugyanakkora
nagyságú sebességgel halad egymás felé vízszintes egyenesen. Tökéletesen rugalmas ütközés után az egyik golyó nyugalomban marad. Mekkora lesz a másik golyó ütközés előtti és utáni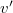 
sebességeinek aránya? Mekkora a golyók tömegeinek aránya?
Megoldás
- Tökéletesen rugalmas ütközés során a két golyó teljes impulzusa és teljes kinetikus energiája is megmarad. Az egyenletrendszert megoldva
![\[m_{1}v-m_{2}v=m_{2}v'\qquad\qquad \frac{1}{2}m_{1}v^{2}+\frac{1}{2}m_{2}v^{2}=\frac{1}{2}m_{2}v'^{2}\]](/images/math/d/5/6/d56fe028e6d64e84da8cd48cc49914d5.png)
![\[m_{1}=3m_{2}\qquad\qquad \frac{v'}{v}=2\,.\]](/images/math/0/4/4/0443359e063bd9894b25af280f9dfd7b.png)
- Tökéletesen rugalmas ütközés során a két golyó teljes impulzusa és teljes kinetikus energiája is megmarad.
