„Pontrendszerek - 3.1.6” változatai közötti eltérés
A Fizipedia wikiből
| 9. sor: | 9. sor: | ||
== Feladat == | == Feladat == | ||
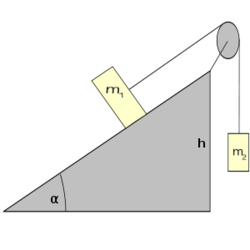
</noinclude><wlatex># (3.1.6) Egy $\alpha=30^\circ$ hajlásszögű lejtőre helyezett $m_{1}=3\,\mathrm{kg}$ tömegű testhez a lejtő tetején megerősített csigán átvetett fonállal $m_{2}=1\,\mathrm{kg}$ tömegű testet kötünk. (3.1.6. ábra) Határozzuk meg a rendszer gyorsulását, valamint a fonalat feszítő erőt! Mekkora sebességet ér el a $h=0,2\,\mathrm{m}$ magasságú lejtő tetejéről kezdősebesség nélkül induló test a lejtő alján? A csiga és a fonál tömegétől, valamint a súrlódástól eltekintünk.[[Kép:Kfgy1_07_3_1_6.svg|none|250px]] | </noinclude><wlatex># (3.1.6) Egy $\alpha=30^\circ$ hajlásszögű lejtőre helyezett $m_{1}=3\,\mathrm{kg}$ tömegű testhez a lejtő tetején megerősített csigán átvetett fonállal $m_{2}=1\,\mathrm{kg}$ tömegű testet kötünk. (3.1.6. ábra) Határozzuk meg a rendszer gyorsulását, valamint a fonalat feszítő erőt! Mekkora sebességet ér el a $h=0,2\,\mathrm{m}$ magasságú lejtő tetejéről kezdősebesség nélkül induló test a lejtő alján? A csiga és a fonál tömegétől, valamint a súrlódástól eltekintünk.[[Kép:Kfgy1_07_3_1_6.svg|none|250px]] | ||
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!}}{{Végeredmény|content= $a=1,25\,\mathrm{\frac{m}{s^{2}}}\qquad K=11,25\,\mathrm{N}$ <br> $v= | + | </wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!}}{{Végeredmény|content= $a=1,25\,\mathrm{\frac{m}{s^{2}}}\qquad K=11,25\,\mathrm{N}$ <br> $v=1\,\mathrm{\frac{m}{s}}$ }}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Az $m_{1}$ tömegű testre a lejtővel párhuzamosan egy $m_{1}g\sin\alpha$ erő és a $K$ kötélerő hat. Az $m_{2}$ tömegű testre függőleges irányban hat a gravitációs erő és egy a fonál nyújthatatlansága miatt ugyanolyan $K$ nagyságú kötélerő. A két test gyorsulása azonos nagyságú. A mozgásegyenletek $$m_{1}a=m_{1}g\sin\alpha-K$$ $$m_{2}a=K-m_{2}g$$ Az egyenlet rendszer alapján $$a=\frac{m_{1}\sin\alpha-m_{2}}{m_{1}+m_{2}}g=1,25\,\mathrm{\frac{m}{s^{2}}}\qquad\qquad K=11,25\,\mathrm{N}\,.$$ A $h$ | + | <wlatex>#: Az $m_{1}$ tömegű testre a lejtővel párhuzamosan egy $m_{1}g\sin\alpha$ erő és a $K$ kötélerő hat. Az $m_{2}$ tömegű testre függőleges irányban hat a gravitációs erő és egy a fonál nyújthatatlansága miatt ugyanolyan $K$ nagyságú kötélerő. A két test gyorsulása azonos nagyságú. A mozgásegyenletek $$m_{1}a=m_{1}g\sin\alpha-K$$ $$m_{2}a=K-m_{2}g$$ Az egyenlet rendszer alapján $$a=\frac{m_{1}\sin\alpha-m_{2}}{m_{1}+m_{2}}g=1,25\,\mathrm{\frac{m}{s^{2}}}\qquad\qquad K=11,25\,\mathrm{N}\,.$$ A $h$ magasságú lejtőn a megtett út $h/\sin\alpha$, így a lejtő alján a test sebessége $$v=\sqrt{2a\frac{h}{\sin\alpha}}=1\,\mathrm{\frac{m}{s}}$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. október 29., 08:14-kori változata
Feladat
- (3.1.6) Egy
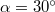hajlásszögű lejtőre helyezett 
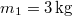tömegű testhez a lejtő tetején megerősített csigán átvetett fonállal 
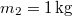tömegű testet kötünk. (3.1.6. ábra) Határozzuk meg a rendszer gyorsulását, valamint a fonalat feszítő erőt! Mekkora sebességet ér el a 
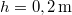magasságú lejtő tetejéről kezdősebesség nélkül induló test a lejtő alján? A csiga és a fonál tömegétől, valamint a súrlódástól eltekintünk.
Megoldás
- Az
tömegű testre a lejtővel párhuzamosan egy 
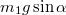erő és a 
kötélerő hat. Az 
tömegű testre függőleges irányban hat a gravitációs erő és egy a fonál nyújthatatlansága miatt ugyanolyan nagyságú kötélerő. A két test gyorsulása azonos nagyságú. A mozgásegyenletek ![\[m_{1}a=m_{1}g\sin\alpha-K\]](/images/math/7/b/a/7baf7bc4fa3d8371d098a09158d36037.png)
Az egyenlet rendszer alapján![\[m_{2}a=K-m_{2}g\]](/images/math/8/c/0/8c0ef3eecba4543b03dde9334390bd96.png)
A![\[a=\frac{m_{1}\sin\alpha-m_{2}}{m_{1}+m_{2}}g=1,25\,\mathrm{\frac{m}{s^{2}}}\qquad\qquad K=11,25\,\mathrm{N}\,.\]](/images/math/b/d/a/bdaf3d59273190a9cf24602cbc9a8cec.png)
magasságú lejtőn a megtett út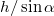 
, így a lejtő alján a test sebessége ![\[v=\sqrt{2a\frac{h}{\sin\alpha}}=1\,\mathrm{\frac{m}{s}}\]](/images/math/5/7/4/574f00db412a3ac823eef8659806e5d0.png)
- Az
