„Mechanika - Gömb felületén lévő tengellyel” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (3.2.4.) $R$ sugarú $m$ tömegű gömböt egy, sugarának gömbfelület menti végpontján átmenő tengely körül megforgatunk. | + | </noinclude><wlatex># (*3.2.4.) $R$ sugarú $m$ tömegű gömböt egy, sugarának gömbfelület menti végpontján átmenő tengely körül megforgatunk. |
#: a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan $\theta_{\text{TKP}}=\frac25mR^2$? | #: a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan $\theta_{\text{TKP}}=\frac25mR^2$? | ||
#: b) Mekkora nyomatékra van szükség ahhoz, hogy $\beta$ nagyságú szöggyorsulással tudjuk forgásba hozni? | #: b) Mekkora nyomatékra van szükség ahhoz, hogy $\beta$ nagyságú szöggyorsulással tudjuk forgásba hozni? | ||
A lap jelenlegi, 2012. november 8., 15:15-kori változata
Feladat
- (*3.2.4.)
sugarú 
tömegű gömböt egy, sugarának gömbfelület menti végpontján átmenő tengely körül megforgatunk.
- a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan
?
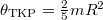- b) Mekkora nyomatékra van szükség ahhoz, hogy
nagyságú szöggyorsulással tudjuk forgásba hozni?
- c) Hogyan kell változni az idő függvényében azon energiaforrás teljesítményének, amely az állandó szöggyorsulást biztosítani képes, ha a gömb a
időpontban nyugalomból indult?
- a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan
Megoldás
A megadott tengelyre vonatkoztatott tehetetlenségi nyomaték a Steiner-tétel szerint![\[\theta=\theta_{\rm{TKP}}+mR^2=\frac75mR^2.\]](/images/math/9/d/e/9de73caa8655ddae8dcf243cfef19a32.png)
![\[M=\theta\beta=\frac75mR^2\beta.\]](/images/math/c/d/6/cd6945f9dbd47e4ab7ce04e7e066390e.png)
időpontban szükséges pillanatnyi teljesítmény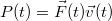 
analógiájára 
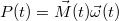, amelyben a vektorok most egyirányúak és 
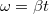, így ![\[P(t)=\frac75mR^2\beta^2t.\]](/images/math/4/6/7/467595248901aee1cf9b42514dd518c2.png)
![\[E_{\text{forg}}=\frac12\theta\omega^2(t)\]](/images/math/2/8/e/28e335f5b1091d36c5e1abece14386f8.png)
