„Pontrendszerek - 3.1.7” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Pontrendszerek {{Kísérleti fizika gyakorl…”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Kétoldalú lejtő felső pontjában rögzített csigán átvetett fonál egyik végéhez kötött $m_{1}=2\,\mathrm{kg}$ tömegű test az $\alpha=30^\circ$, másik végéhez kötött $m_{2}=1\,\mathrm{kg}$ tömegű test a $\beta=45^\circ$ hajlásszögű lejtőn fekszik. (3.1.7. ábra) Határozzuk meg a gyorsulást és a fonalat feszítő erőt, ha a súrlódástól és a csiga tömegétől eltekintünk! | + | </noinclude><wlatex># ÁBRA Kétoldalú lejtő felső pontjában rögzített csigán átvetett fonál egyik végéhez kötött $m_{1}=2\,\mathrm{kg}$ tömegű test az $\alpha=30^\circ$, másik végéhez kötött $m_{2}=1\,\mathrm{kg}$ tömegű test a $\beta=45^\circ$ hajlásszögű lejtőn fekszik. (3.1.7. ábra) Határozzuk meg a gyorsulást és a fonalat feszítő erőt, ha a súrlódástól és a csiga tömegétől eltekintünk! |
</wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!}}{{Végeredmény|content= $a=0,976\,\mathrm{\frac{m}{s^{2}}}\qquad\qquad K=8,05\,\mathrm{N}\,.$ }}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!}}{{Végeredmény|content= $a=0,976\,\mathrm{\frac{m}{s^{2}}}\qquad\qquad K=8,05\,\mathrm{N}\,.$ }}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap 2013. április 22., 19:55-kori változata
Feladat
- ÁBRA Kétoldalú lejtő felső pontjában rögzített csigán átvetett fonál egyik végéhez kötött
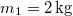tömegű test az 
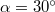, másik végéhez kötött 
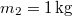tömegű test a 
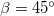hajlásszögű lejtőn fekszik. (3.1.7. ábra) Határozzuk meg a gyorsulást és a fonalat feszítő erőt, ha a súrlódástól és a csiga tömegétől eltekintünk!
Megoldás
- A két test mozgásegyenlete Ezek alapján
![\[m_{1}a=m_{1}g\sin\alpha-K\qquad\qquad m_{2}a=K-m_{2}g\sin\beta\,.\]](/images/math/6/3/d/63d1554182af3fa8fc1eddf1d72aa039.png)
![\[a=\frac{m_{1}\sin\alpha-m_{2}\sin\beta}{m_{1}+m_{2}}g=0,976\,\mathrm{\frac{m}{s^{2}}}\qquad\qquad K=8,05\,\mathrm{N}\,.\]](/images/math/5/8/5/5857fb3653ed49cff8b26b4745acdac3.png)
- A két test mozgásegyenlete
