„Pontrendszerek - 3.1.13” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Pontrendszerek {{Kísérleti fizika gyakorl…”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy $M=70\,\mathrm{kg}$ tömegű ember kezében $m=10\,\mathrm{kg}$ tömegű teherrel a vízszintessel $45^\circ$-os szöget bezáró irányban $v_{0}=7\,\mathrm{m/s}$ kezdősebességgel felugrik. Pályája tetőpontján a terhet vízszintes $u=8\,\mathrm{m/s}$ relatív sebességgel hátrafelé hajítja. Mennyivel nagyobb távolságra ugrik ily módon? | + | </noinclude><wlatex># (3.1.13) Egy $M=70\,\mathrm{kg}$ tömegű ember kezében $m=10\,\mathrm{kg}$ tömegű teherrel a vízszintessel $45^\circ$-os szöget bezáró irányban $v_{0}=7\,\mathrm{m/s}$ kezdősebességgel felugrik. Pályája tetőpontján a terhet vízszintes $u=8\,\mathrm{m/s}$ relatív sebességgel hátrafelé hajítja. Mennyivel nagyobb távolságra ugrik ily módon? |
</wlatex><includeonly><wlatex>{{Útmutatás|content=Az eldobás leírásához érdemes figyelembe venni az impulzus megmaradást!}}{{Végeredmény|content=$\Delta s=0,566\,\mathrm{m}$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=Az eldobás leírásához érdemes figyelembe venni az impulzus megmaradást!}}{{Végeredmény|content=$\Delta s=0,566\,\mathrm{m}$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap jelenlegi, 2013. augusztus 27., 21:39-kori változata
Feladat
- (3.1.13) Egy
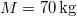 tömegű ember kezében
tömegű ember kezében 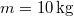 tömegű teherrel a vízszintessel
tömegű teherrel a vízszintessel 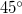 -os szöget bezáró irányban
-os szöget bezáró irányban 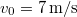 kezdősebességgel felugrik. Pályája tetőpontján a terhet vízszintes
kezdősebességgel felugrik. Pályája tetőpontján a terhet vízszintes 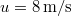 relatív sebességgel hátrafelé hajítja. Mennyivel nagyobb távolságra ugrik ily módon?
relatív sebességgel hátrafelé hajítja. Mennyivel nagyobb távolságra ugrik ily módon?
Megoldás
- A felugráskor az ember sebességének vízszintes és függőleges komponense Ha nem dobja el a terhet az ugrás során, akkor
![\[v_{x}=v_{0}\cos\alpha\qquad\qquad v_{y}=v_{0}\sin\alpha\]](/images/math/2/d/8/2d8260fec9f1ad8f2cfa0dcc8788d54d.png) távolságig ugrik. Ha a terhet a pályája legfelső pontján eldobja, akkor az eldobás után a sebessége
távolságig ugrik. Ha a terhet a pályája legfelső pontján eldobja, akkor az eldobás után a sebessége![\[s=2v_{x}\frac{v_{y}}{g}\]](/images/math/8/4/0/84063d0184b1cc3b098cb3fbfdbdf934.png)
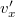 lesz, melyet az impulzus megmaradás segítségével számíthatunk ki, hiszen nem hatnak vízszintes irányú külső erők az eldobás pillanatában. Ebben az esetben
lesz, melyet az impulzus megmaradás segítségével számíthatunk ki, hiszen nem hatnak vízszintes irányú külső erők az eldobás pillanatában. Ebben az esetben![\[(m+M)v_{x}=Mv_{x}'-m(u-v_{x})\qquad\Rightarrow\qquad v_{x}'=\frac{mu+M v_{x}}{M}\]](/images/math/1/e/b/1eb1aeb0c15c1b478d9a38f676deba43.png) távolságig ugrik. A két távolság különbsége
távolságig ugrik. A két távolság különbsége![\[s'=(v_{x}+v_{x}')\frac{v_{y}}{g}\]](/images/math/b/c/0/bc0d29425366b29442a3eebd245d571c.png)
![\[\Delta s=s'-s=\frac{muv_{0}\sin\alpha}{Mg}=0,566\,\mathrm{m}\,.\]](/images/math/c/2/6/c269203faf0f744dd63c8f8e403e4be8.png)
- A felugráskor az ember sebességének vízszintes és függőleges komponense