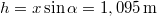„Mechanika - Falhoz támasztott létra” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Feladat) |
||
| 9. sor: | 9. sor: | ||
== Feladat == | == Feladat == | ||
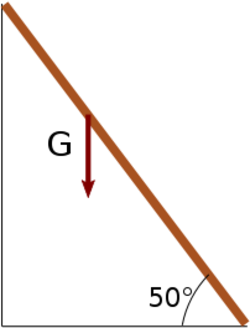
</noinclude><wlatex># (*3.2.14.) Egy $4\,\rm m$ hosszú létrát függőleges falhoz támasztunk úgy, hogy a vízszintes talajjal $50^{\circ}$-os szöget zár be. A létra és a talaj közötti súrlódási együttható $0,3$. A fal súrlódásmentes. Ha valaki a létrára mászik, milyen magasra jut, mielőtt a létra megcsúszik? (A létra tömegét hanyagoljuk el!) | </noinclude><wlatex># (*3.2.14.) Egy $4\,\rm m$ hosszú létrát függőleges falhoz támasztunk úgy, hogy a vízszintes talajjal $50^{\circ}$-os szöget zár be. A létra és a talaj közötti súrlódási együttható $0,3$. A fal súrlódásmentes. Ha valaki a létrára mászik, milyen magasra jut, mielőtt a létra megcsúszik? (A létra tömegét hanyagoljuk el!) | ||
| − | [[Kép:3.2. | + | [[Kép:3.2.14.svg|none|250px]] |
</wlatex><includeonly><wlatex>{{Útmutatás|content=A nyomatéki egyenletet arra a pontra nézve érdemes felírni, ahol a legtöbb az ismeretlen erő.}}{{Végeredmény|content=$$h=1,095\,\rm m$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=A nyomatéki egyenletet arra a pontra nézve érdemes felírni, ahol a legtöbb az ismeretlen erő.}}{{Végeredmény|content=$$h=1,095\,\rm m$$}}</wlatex></includeonly><noinclude> | ||
A lap 2013. június 30., 15:00-kori változata
Feladat
- (*3.2.14.) Egy
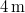 hosszú létrát függőleges falhoz támasztunk úgy, hogy a vízszintes talajjal
hosszú létrát függőleges falhoz támasztunk úgy, hogy a vízszintes talajjal 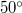 -os szöget zár be. A létra és a talaj közötti súrlódási együttható
-os szöget zár be. A létra és a talaj közötti súrlódási együttható 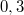 . A fal súrlódásmentes. Ha valaki a létrára mászik, milyen magasra jut, mielőtt a létra megcsúszik? (A létra tömegét hanyagoljuk el!)
. A fal súrlódásmentes. Ha valaki a létrára mászik, milyen magasra jut, mielőtt a létra megcsúszik? (A létra tömegét hanyagoljuk el!)
Megoldás
A létra hossza legyen , a felmászó ember súlyereje
, a felmászó ember súlyereje 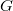 , a létra tetejénél ható falra merőleges támasztó erő
, a létra tetejénél ható falra merőleges támasztó erő  , az aljánál pedig
, az aljánál pedig 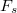 súrlódási erő és
súrlódási erő és  nyomóerő hat. Az erők egyensúlya vízszintesen és függőlegesen
nyomóerő hat. Az erők egyensúlya vízszintesen és függőlegesen 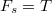 illetve
illetve 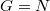 . A nyomatéki egyenletet a létra alján érdemes felírni. Ha az ember a létrán x távolságra mászott fel,
. A nyomatéki egyenletet a létra alján érdemes felírni. Ha az ember a létrán x távolságra mászott fel, 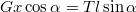 . Az erőegyenletek alapján a nyomatéki egyenletet átírva kapjuk
. Az erőegyenletek alapján a nyomatéki egyenletet átírva kapjuk ![\[F_s=\frac{Nx\cot{\alpha}}l,\]](/images/math/3/b/9/3b9826462b3aa2168d7e2eeac520b44b.png)
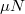 -el egyenlő, így a nyomóerővel egyszerűsíthetünk. A létrán tehát
-el egyenlő, így a nyomóerővel egyszerűsíthetünk. A létrán tehát 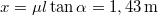 távolságba mászhatunk, ami magasságban
távolságba mászhatunk, ami magasságban