„Elektrosztatika - Vezetőképesség, áramsűrűség” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika gyakorlat 2. | gyaks…”) |
|||
| 4. sor: | 4. sor: | ||
| tárgynév = Kísérleti fizika gyakorlat 2. | | tárgynév = Kísérleti fizika gyakorlat 2. | ||
| gyaksorszám = 5 | | gyaksorszám = 5 | ||
| − | | témakör = Elektrosztatika - Vezetőképesség, áramsűrűség | + | | témakör = Elektrosztatika - Vezetőképesség, áramsűrűség |
}} | }} | ||
== Feladatok == | == Feladatok == | ||
| − | {{:Elektrosztatika példák - | + | {{:Elektrosztatika példák - Vezető anyaggal töltött kondenzátor ellenállása}}{{Megoldás|link=Elektrosztatika példák - Vezető anyaggal töltött kondenzátor ellenállása}} |
| − | + | {{:Elektrosztatika példák - Változó vezetőképességű anyaggal töltött kocka ellenállása}}{{Megoldás|link=Elektrosztatika példák - Változó vezetőképességű anyaggal töltött kocka ellenállása}} | |
| − | + | {{:Elektrosztatika példák - Határfelületen kialakult töltéssűrűség}}{{Megoldás|link=Elektrosztatika példák - Határfelületen kialakult töltéssűrűség}} | |
| − | + | {{:Elektrosztatika példák - Vezető anyaggal töltött síkkondenzátor töltéseloszlása}}{{Megoldás|link=Elektrosztatika példák - Vezető anyaggal töltött síkkondenzátor töltéseloszlása}} | |
| − | + | {{:Elektrosztatika példák - Áramvonalak törési törvénye}{{Megoldás|link=Elektrosztatika példák - Áramvonalak törési törvénye}} | |
| − | + | ||
| − | {{:Elektrosztatika példák - | + | |
| − | {{:Elektrosztatika példák - | + | |
| − | {{:Elektrosztatika példák - | + | |
| − | + | ||
| − | {{:Elektrosztatika példák - | + | |
| − | + | ||
A lap 2013. július 1., 17:39-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 2. |
Gyakorlatok listája:
|
| Elektrosztatika - Vezetőképesség, áramsűrűség |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- Számítsuk ki az
a)
és 
sugarú gömblemezekből álló 
, 
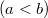vezetőképességű közeggel kitöltött gömbkondenzátor; ill.
b) az
hosszúságú, és sugarú, fegyverzetekből álló, vezetőképességű közeggel kitöltött hengerkondenzátor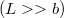 
ellenállását!
A fegyverzetek közti feszültség mindkét esetben időben állandó!Végeredménya)![\[R = \frac{U}{I} = \frac{1}{4 \pi\sigma}\cdot\frac{b-a}{ab}\]](/images/math/8/4/e/84e92eab27c675b0f15ff3e48ae19305.png)
b)![\[R = \frac{U}{I} = \frac{\ln\left(\frac{b}{a}\right)}{2 \pi L\sigma}\]](/images/math/2/c/0/2c03bec5c484c7acbeff168450f84864.png)
- Egy élhosszúságú kocka anyagának vezetőképessége a magasság függvényében így változik:Számítsuk ki a kocka ellenállását
![\[\sigma = \sigma_0\cdot\frac{2a-z}{a}\]](/images/math/f/d/2/fd2be9690057ff7b44baf29fff534491.png)
a) az alsó és felső;
b) a két átellenes, oldalsó lap között.Végeredménya)![\[R = \frac{U}{I} = \frac{\ln\left(2\right)}{\sigma_0 a}\]](/images/math/d/8/0/d80263204117fffda3b7802dc8ae4071.png)
b)![\[R = \frac{U}{I} = \frac{2}{3}\cdot\frac{1}{a \sigma_0}\]](/images/math/9/0/a/90a6b8c81711ff8f24702692d022b09b.png)
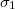és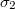 
vezetőképességű anyagok érintkező felületén normális irányú áramsűrűség folyik át. Határozzuk meg a felületi töltéssűrűséget!Végeredmény![\[W=\dfrac{4 \rho^2 \pi R^5}{15 \varepsilon_0}\]](/images/math/4/c/9/4c9cb38d1d2f29cddb52eb3204968e09.png)
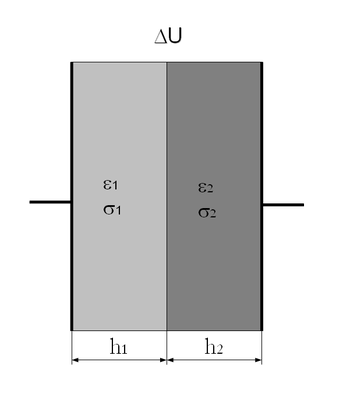
- Egy síkkondenzátor fegyverzetek közötti terét két vezető lemezzel töltjük ki. A lemezek egymással és a kondenzátor lemezeivel teljes felületükön érintkeznek. A lemezek vastagsága
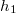és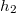 
, vezetőképességük és dielektromos állandójuk 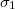,,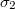 illetve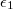 
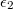. A kondenzátorlemezek (melyek 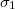-nél és 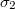-nél jóval nagyobb vezetőképességű anyagból készültek) között adott a potenciálkülönbség: 
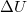. Határozzuk meg az elektromos tér, valamint az elektromos eltolás nagyságát! Határozzuk meg az áramsűrűség nagyságát a közegekben, továbbá a stacionárius áramok hatására kialakuló felületi töltéssűrűséget! A síkkondenzátort ideálisnak tételezzük fel, azaz a szélein kialakuló szórt tértől tekintsünk el!
Végeredmény.![\[D_2 A-D_1 A =\omega A \rightarrow \omega = D_2-D_1 = \frac{\Delta U\epsilon_0\cdot \left(\epsilon_2\sigma_1-\epsilon_1\sigma_2\right)}{\sigma_2 h_1+\sigma_1 h_2} \]](/images/math/b/f/f/bffca100570ab77a7406e9d7e645c11c.png)
