Magnetosztatika - Mágneses tér energiája. Váltakozó áram, eltolási áram
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 2. |
Gyakorlatok listája:
|
| Magnetosztatika - Mágneses tér energiája. Váltakozó áram, eltolási áram |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- Egy
 menetes toroid vasmagjában
menetes toroid vasmagjában  áramerősség hatására
áramerősség hatására 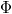 fluxus jön létre. Mekkora a mágneses tér energiája?
fluxus jön létre. Mekkora a mágneses tér energiája?
- Egy
 középsugarú,
középsugarú,  keresztmetszetű vasgyűrűre
keresztmetszetű vasgyűrűre  menetet tekercselnek. A gyűrűn
menetet tekercselnek. A gyűrűn  széles légrést alakítanak ki. A használatos gerjesztő áramoknál a vas relatív permeabilitása
széles légrést alakítanak ki. A használatos gerjesztő áramoknál a vas relatív permeabilitása 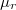 . Határozzuk meg a légrésben és a vasmagban tárolt energia arányát! Az energiából mekkora öninduktivitás számolható?
. Határozzuk meg a légrésben és a vasmagban tárolt energia arányát! Az energiából mekkora öninduktivitás számolható?
- Egy
 induktivitású és
induktivitású és  ellenállású tekercset egy
ellenállású tekercset egy  elektromotoros erejű telephez kapcsolunk. Mennyi idő alatt éri el az áram az állandósult értékének az
elektromotoros erejű telephez kapcsolunk. Mennyi idő alatt éri el az áram az állandósult értékének az 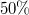 -át?
-át?
- Egy
 induktivitású tekercset és egy
induktivitású tekercset és egy  ellenállást egy
ellenállást egy  frekvenciával szinuszosan változó feszültségű forrásra kapcsolunk. Mekkora
frekvenciával szinuszosan változó feszültségű forrásra kapcsolunk. Mekkora 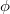 szöggel késik az áram a feszültséghez képest?
szöggel késik az áram a feszültséghez képest?
- Határozzuk meg, mekkora az eltolási áram egy olyan síkkondenzátor esetén, amelynek lemezei egymással párhuzamosak maradnak, miközben
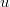 sebességgel távolodnak egymástól, ha
sebességgel távolodnak egymástól, ha
a) az töltéssűrűség állandó
töltéssűrűség állandó
b) a lemezek közötti feszültség állandó.
- Mekkora egy S keresztmetszetű ideális síkkondenzátor lemezei között az elektromos térerősség maximális értéke, ha a kondenzátorra kapcsolt áram szinuszosan váltakozik: Vagyis
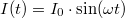
- Hosszú, egyenes szolenoid hosszegységenként
 menettel rendelkezik, és
menettel rendelkezik, és 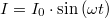 erősségű váltakozó áram járja át. Határozzuk meg az eltolási áramsűrűséget a szolenoid tengelyétől mért távolság függvényében, ha szolenoid keresztmetszetének sugara
erősségű váltakozó áram járja át. Határozzuk meg az eltolási áramsűrűséget a szolenoid tengelyétől mért távolság függvényében, ha szolenoid keresztmetszetének sugara  !
!
![\[E = \frac{1}{2}LI = \frac{1}{2}N\Phi I\]](/images/math/4/b/9/4b9e6a868b139866c729730df6b4d505.png)
![\[\frac{E_{leg}}{E_{vas}} = \frac{\mu_r b}{\left(2\pi r-b\right)}\]](/images/math/d/3/7/d37c39ad80f80ddcae126c5cc7eb8405.png)
![\[L = \frac{N^2\mu_0\mu_r A}{2 \pi r+b\left(\mu_r-1\right)}\]](/images/math/1/f/b/1fbdded5087fa1d43442212635ccda8f.png)
![\[t = -\frac{L}{R}\ln\left(0.5\right)\]](/images/math/4/8/1/481d84668ebc507feb6a27b633dd9ffc.png)
![\[\phi = \arctan\left(\frac{L\omega}{R}\right)\]](/images/math/8/7/5/875a979fd12d84007a5bd9415b809b90.png)
![\[\frac{\partial D}{\partial t} = 0\]](/images/math/1/c/c/1cc2bd06331a5f4b5abd0bb327a36516.png)
![\[\frac{\partial D}{\partial t} = -\frac{U \epsilon_0}{ut^2}\]](/images/math/0/b/4/0b4c599dac950846ccaeceb05815b655.png)
![\[E = \frac{I_0}{\omega\epsilon_0 S}\]](/images/math/3/1/c/31ce9a1548e452ed65b48e583dca447e.png)
![\[\frac{\partial D}{\partial t}= \frac{1}{2}\mu_0 \epsilon_0 I_0 \omega^2 r n \sin\left(\omega t \right)\]](/images/math/0/8/b/08b7cf958b52b50fad02493e6c45ec19.png)