Magnetosztatika példák - Fáziskésés váltakozó-áramú LR körben

Feladat

1. Egy $\setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0%$ induktivitású tekercset és egy $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ ellenállást egy $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ frekvenciával szinuszosan változó feszültségű forrásra kapcsolunk. Mekkora 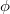$\setbox0\hbox{$\phi$}% \message{//depth:\the\dp0//}% \box0%$ szöggel késik az áram a feszültséghez képest?

Megoldás

Ha felírjuk a hurok-törvényt erre az áramkörre, akkor a következő differenciál egyenletet kapjuk:

$\[U = RI + L\dot{I}\]$

Egyszerűen kezelhetjük a problémát, ha bevezetjük a komplex áramot és feszültséget. A valóságban a mérhető áram és feszültség természetesen valós, időben harmonikus függvény szerint változik, de a fázisviszonyok egyszerű számítása érdekében érdemes komplex formalizmust alkalmazni. Tehát a forrás feszültsége legyen:

$\[U = \tilde{U}e^{i\omega t}\]$

ahol $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ a váltakozó áram körfrekvenciája. Keressük a megoldást a következő alakban:

$\[I = \tilde{I}e^{i\omega t}\]$

Ezt behelyettesítve és 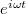$\setbox0\hbox{$e^{i\omega t}$}% \message{//depth:\the\dp0//}% \box0%$-vel leegyszerűsítve:

$\[\tilde{U} = \tilde{I}\left(R+iL\omega\right)\]$

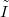Amit ha $\setbox0\hbox{$\tilde{I}$}% \message{//depth:\the\dp0//}% \box0%$-re rendezünk, akkor:

$\[\tilde{I}=\frac{\tilde{U}}{R+iL\omega}\]$

Ha feszültség fázisát zérusnak vesszük (hiszen hozzá képest mérjük az áram fázisát), akkor a feszültséget vehetjük valós értékűnek:

$\[\tilde{I} = \frac{U}{R+iL\omega} = \frac{U\left(R-iL\omega\right)}{R^2-L^2\omega^2}\]$

Ebből látjuk, hogy

$\[\text{Re}(\tilde{I}) = \frac{U(R)}{R^2-L^2\omega^2}\]$

és

$\[\text{Im}(\tilde{I}) = \frac{U(-L\omega)}{R^2-L^2\omega^2}\]$

.

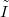Innen $\setbox0\hbox{$\tilde{I}$}% \message{//depth:\the\dp0//}% \box0%$ fázisa a feszültséghez képest:

$\[\phi = -\arctan\left(\frac{\text{Im}(\tilde{I})}{\text{Re}(\tilde{I})}\right) = -\arctan\left(\frac{L\omega}{R}\right)\]$

Tehát ennyivel késik az áram a feszültséghez képest.