Magnetosztatika - Az indukció törvénye, mozgási indukció
A Fizipedia wikiből
(Magnetosztatika - Mozgási indukció szócikkből átirányítva)
Feladatok
 indukciójú homogén mágneses erőtérben egyenletesen forog egy
indukciójú homogén mágneses erőtérben egyenletesen forog egy  menetű tekercs, a tekercs tengelyére és a mágneses erőtérre is merőleges tengely körül. A tekercs forgásának frekvenciája
menetű tekercs, a tekercs tengelyére és a mágneses erőtérre is merőleges tengely körül. A tekercs forgásának frekvenciája  , a keresztmetszete pedig
, a keresztmetszete pedig  . Határozzuk meg a tekercs forgása közben indukált maximális elektromotoros erőt!
. Határozzuk meg a tekercs forgása közben indukált maximális elektromotoros erőt!
- Egy
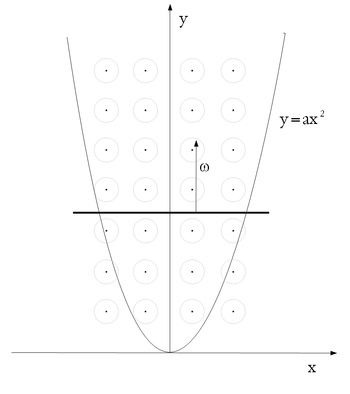
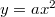 egyenletnek megfelelően parabola alakúra hajlított vezetőt az xy síkra merőleges
egyenletnek megfelelően parabola alakúra hajlított vezetőt az xy síkra merőleges  mágneses indukciójú térbe helyezzük. A
mágneses indukciójú térbe helyezzük. A 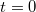 pillanatban az x tengellyel párhuzamos vezető
pillanatban az x tengellyel párhuzamos vezető 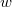 gyorsulással elindul az
gyorsulással elindul az 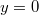 helyzetből a pozitív
helyzetből a pozitív  irányban. Állapítsuk meg az indukált feszültséget y függvényeként.
irányban. Állapítsuk meg az indukált feszültséget y függvényeként.
- Egy
 sugarú hosszegységenként
sugarú hosszegységenként  menetű, hosszú tekercsben
menetű, hosszú tekercsben  áram folyik. Ennek a tekercsnek a közepébe helyezünk egy koaxiális, azonos keresztmetszetű,
áram folyik. Ennek a tekercsnek a közepébe helyezünk egy koaxiális, azonos keresztmetszetű,  menetű,
menetű,  ellenállással lezárt tekercset. Mennyi töltés fog áthaladni a második tekercsen, ha az elsőben az áram irányát
ellenállással lezárt tekercset. Mennyi töltés fog áthaladni a második tekercsen, ha az elsőben az áram irányát  idő alatt egyenletesen az ellenkezőjére változtatjuk?
idő alatt egyenletesen az ellenkezőjére változtatjuk?
- Egy végtelen hosszúnak tekinthető egyenes vezetőben
 áram folyik. A vezetőtől
áram folyik. A vezetőtől  ill.
ill.  távolságban vele párhuzamosan elhelyezett két vezető egyik vége egy
távolságban vele párhuzamosan elhelyezett két vezető egyik vége egy  ellenálláson keresztül össze van kötve. A két párhuzamos vezetőn egy rájuk merőlegesen elhelyezett vezetőt csúsztatunk
ellenálláson keresztül össze van kötve. A két párhuzamos vezetőn egy rájuk merőlegesen elhelyezett vezetőt csúsztatunk  sebességgel.
sebességgel.
a) Határozza meg a vezető keretben indukált áram irányát és nagyságát. (A vezetők ellenállása elhanyagolható)
b) Állapítsa meg az az erőt, amely az állandó sebesség fenntartásához szükséges, valamint az áramot szállító vezetőtől azt az
áramot szállító vezetőtől azt az  távolságot, ahol ennek az erőnek támadnia kell!
távolságot, ahol ennek az erőnek támadnia kell!
c) Határozza meg a vezető mozgatásához szükséges teljesítményt.
- Küllős fémtárcsát forgassunk homogén mágneses erőtérben az erővonalakkal párhuzamos tengely körül. Mekkora feszültség mérhető a tárcsa tengelye és pereme között? A tárcsa sugara
 , a mágneses indukció
, a mágneses indukció  a fordulatszám
a fordulatszám  .
.
- Hosszegységenként
 ellenállású vezetéket úgy hajlítunk meg, hogy az ábrán látható módon
ellenállású vezetéket úgy hajlítunk meg, hogy az ábrán látható módon 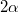 szöget alkosson. Egy könnyen csúszó rudat helyezünk az így kialakított sínre úgy, hogy ABC egyenlőszárú háromszöget alkot. A rúd ugyanabból a vezetőből készült, mint a sín. Az elrendezést a síkjára merőleges, homogén
szöget alkosson. Egy könnyen csúszó rudat helyezünk az így kialakított sínre úgy, hogy ABC egyenlőszárú háromszöget alkot. A rúd ugyanabból a vezetőből készült, mint a sín. Az elrendezést a síkjára merőleges, homogén  indukciójú térbe helyezzük. Mekkora áram folyik a hurokban, amikor a rúd
indukciójú térbe helyezzük. Mekkora áram folyik a hurokban, amikor a rúd  sebességgel mozog? (A kontaktusoknál fellépő ellenállásoktól tekintsünk el.)
sebességgel mozog? (A kontaktusoknál fellépő ellenállásoktól tekintsünk el.)
- Egy vezeték súlódásmentesen csúszhat egy vízszinesen elhelyezkedő
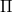 alakú vezetőhurkon. A vezető hossza
alakú vezetőhurkon. A vezető hossza  , tömege
, tömege  , ellenállása
, ellenállása  . Az egész rendszer homogén, függőlegesen felfelé irányuló
. Az egész rendszer homogén, függőlegesen felfelé irányuló  mágneses indukciójú térben helyezkedik el. A
mágneses indukciójú térben helyezkedik el. A  pillanatban fellépő, vízszintes erő hatására a vezeték jobbra mozog. Hogyan változik a vezeték sebessége az idő függvényében. (Az áramhurok induktivitása, és a
pillanatban fellépő, vízszintes erő hatására a vezeték jobbra mozog. Hogyan változik a vezeték sebessége az idő függvényében. (Az áramhurok induktivitása, és a 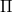 alakú vezető ellenállása elhanyagolható.
alakú vezető ellenállása elhanyagolható.
![\[U_{max} = 2\pi fBNA\]](/images/math/3/2/3/32323b001e55e903c45abcf94c14801b.png)
![\[U = -B\cdot\sqrt{\frac{2w}{a}}\cdot y \]](/images/math/8/a/2/8a2664d717dcdbbfad6b9f6c7486eb30.png)
![\[Q = \frac{2\mu_0 n N I r^2 \pi}{R}\]](/images/math/6/f/5/6f53a84f888d8ba238b4d7b13e323b98.png)
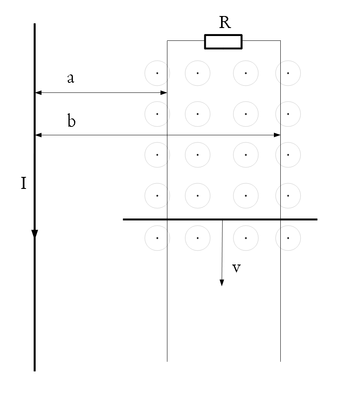
![\[I_{ind} = \frac{U}{R} = - \frac{\mu_0 I v}{2\pi R}\ln\left(\frac{b}{a}\right)\]](/images/math/1/2/9/129f9d1611e56f9d1046d25dd8869af5.png)
![\[F = \int_a^b \frac{\mu_0 I_{ind} I}{2\pi r} dr = \frac{\mu_0 I_{ind} I}{2\pi}\ln\left(\frac{b}{a}\right)\]](/images/math/a/8/8/a88de52d87a8c80b7367335aaa00f231.png)
![\[x = \frac{(b-a)}{\ln\left(\frac{b}{a}\right)}\]](/images/math/e/3/3/e3370cda2767b2272fe2466aa08242cd.png)
![\[P = \frac{\mu_0^2 I^2}{4\pi^2 R}\ln\left(\frac{b}{a}\right)^2 v^2 = U\cdot I\]](/images/math/b/8/e/b8e99a5068516748092147cda749cb64.png)
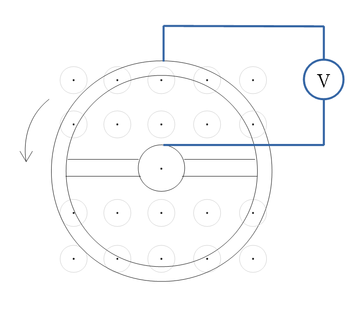
![\[U = \int_0^R E dr = \frac{2\pi n B R^2}{2} \]](/images/math/7/9/8/7989c4762bee70f7e0422e10dde85dd2.png)
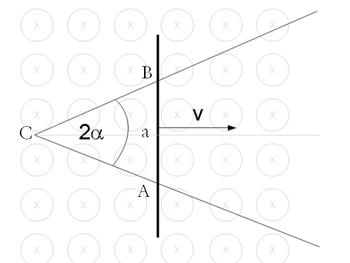
![\[I = \frac{U}{R} =-\frac{ 2 B v^2 t \cdot \tan(\alpha) } {2 v t r \left(\frac{1}{\cos(\alpha)}+\tan(\alpha)\right)} = -\frac{B v \sin(\alpha)}{r \left(1+\sin(\alpha)\right)}\]](/images/math/c/9/1/c91ee547cd486734c5b4f18c9987abbb.png)
![\[v(t) = \frac{F_0 R}{B^2l^2}\left(1-e^{-\frac{B^2l^2}{Rm}t}\right)\]](/images/math/b/1/d/b1dcd1558328098177c1ffe7b9baa958.png)