Magnetosztatika példák - Lezárt sínen állandó erő erővel mozgatott vezető
A Fizipedia wikiből
(Magnetosztatika példák - Vezető keret, Lenz erő szócikkből átirányítva)
Feladat
- Egy vezeték súlódásmentesen csúszhat egy vízszinesen elhelyezkedő
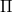 alakú vezetőhurkon. A vezető hossza
alakú vezetőhurkon. A vezető hossza  , tömege
, tömege  , ellenállása
, ellenállása  . Az egész rendszer homogén, függőlegesen felfelé irányuló
. Az egész rendszer homogén, függőlegesen felfelé irányuló  mágneses indukciójú térben helyezkedik el. A
mágneses indukciójú térben helyezkedik el. A  pillanatban fellépő, vízszintes erő hatására a vezeték jobbra mozog. Hogyan változik a vezeték sebessége az idő függvényében. (Az áramhurok induktivitása, és a
pillanatban fellépő, vízszintes erő hatására a vezeték jobbra mozog. Hogyan változik a vezeték sebessége az idő függvényében. (Az áramhurok induktivitása, és a 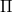 alakú vezető ellenállása elhanyagolható.
alakú vezető ellenállása elhanyagolható.
Megoldás
A vezető rúd mozgásegyenlete a következő:
![\[m\ddot{x} = F_0+F_L\]](/images/math/f/b/3/fb389b978eddc96546720bed8f8eb75c.png)
Ahol 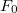 a vezetéket gyorsító konstans erő,
a vezetéket gyorsító konstans erő, 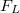 pedig a vezetőre ható Lorentz erő, ami a Lenz-törvény értelmében fékezi a rúd mozgását.
pedig a vezetőre ható Lorentz erő, ami a Lenz-törvény értelmében fékezi a rúd mozgását.
A vezető keretben indukált feszültség:
![\[U -\frac{\partial \Phi}{\partial t} = -\frac{\partial B l x}{\partial t} = - B l \dot{x}\]](/images/math/1/d/9/1d98a50a1e30874fd4fe04bc9a195cea.png)
A vezetékben folyó áram:
![\[I = \frac{U}{R} = \frac{- B l \dot{x}}{R}\]](/images/math/6/6/e/66ea01e877b8364a9bd5059288db7bb6.png)
Mivel a vezeték és a mágneses tér merőlegesek egymásra, ezért a vezetékre ható Lorentz erő nagysága:
![\[F_{L} = BIl = -\frac{B^2l^2}{R}\dot{x}\]](/images/math/2/2/a/22a79313abbe1f5b1c978843f40956b1.png)
Ezzel a rúd mozgásegyenlete:
![\[m\ddot{x} = F_0-\frac{B^2l^2}{R}\dot{x}\]](/images/math/d/4/8/d48a8f946c082a48eec6e1a1fc58c498.png)
Ez egy elsőrendű szétválasztható differenciál egyenlet:
![\[\dot{v} = \frac{F_0}{m}-\frac{B^2l^2}{R m}v\]](/images/math/4/0/5/4050874466974e5cde07cf3a1451827f.png)
Ez kiintegrálható a változók szétválasztásával:
![\[\int_0^v \frac{dv}{\frac{F_0}{m}-\frac{B^2l^2}{Rm}v} = \int_0^t dt\]](/images/math/f/4/6/f4676d1ba4e0f9c5fdeb556ebf7551d7.png)
Amiből a vezeték sebesség időfüggvénye:
![\[v(t) = \frac{F_0 R}{B^2l^2}\left(1-e^{-\frac{B^2l^2}{Rm}t}\right)\]](/images/math/b/1/d/b1dcd1558328098177c1ffe7b9baa958.png)