„Pontrendszerek - 3.1.14” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy súrlódásmentes asztalon $\alpha$ hajlásszögű, $l$ hosszúságú, $M$ tömegű lejtő van. A lejtő tetején egy $m$ tömegű test van. Mekkora távolságra mozdul el a lejtő azalatt míg a test a lejtő aljára csúszik le? | + | </noinclude><wlatex># (3.1.14) Egy súrlódásmentes asztalon $\alpha$ hajlásszögű, $l$ hosszúságú, $M$ tömegű lejtő van. A lejtő tetején egy $m$ tömegű test van. Mekkora távolságra mozdul el a lejtő azalatt míg a test a lejtő aljára csúszik le? |
</wlatex><includeonly><wlatex>{{Útmutatás|content=Gondold végig, hogy milyen (irányú) külső erők hatnak a rendszerre!}}{{Végeredmény|content=$$d=\frac{m}{m+M}l$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=Gondold végig, hogy milyen (irányú) külső erők hatnak a rendszerre!}}{{Végeredmény|content=$$d=\frac{m}{m+M}l$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Rögzítsük a vonatkoztatási rendszert úgy, hogy az $x$- és $y$- tengelyek a lejtő egymásra merőleges oldalaira illeszkednek. Jelöljük $x_{M}$-mel a lejtő tömegközéppontját, amelyet bizonyos esetekben meg is tudnánk határozni, azonban a számolás során nem lesz szükség a pontos értékére. A teljes rendszer tömegközéppontja $$x_{TKP}=\frac{0\cdot m+ x_{M} M}{m+M}\,,$$ amely a mozgás során nem változik, hiszen nincs súrlódás az asztal és a lejtő között, így nem hat semmilyen vízszintes irányú külső erő a rendszerre. Ha a lecsúszás után a lejtő $d$ távolságra tolódott el negatív irányba, akkor a rajta lévő $m$ tömegű test az $l-d$ pozícióba kerül. A végállapotban a tömegközéppont helye $$x_{TKP}=\frac{m(l-d)+M\left(x_{M}-d\right)}{m+M}\,.$$ A két egyenletet összevetve $$d=\frac{m}{m+M}l$$ adódik függetlenül attól, hogy a lejtő homogén-e vagy sem. <br> <br> Megjegyzés: Homogén lejtő esetén ki lehetne számolni a lejtő tömegközéppontjának helyzetét az alábbi számolás szerint. A kezdeti állapotban $$x_{M}=\frac{1}{M}\int_{0}^{l}\int_{0}^{l\,\mbox{tg}\,\alpha\left(1-\frac{x}{l}\right)}\rho(x,y) x dy dx\,,$$ ahol $\rho(x,y)$ a lejtő sűrűsége. Homogén lejtő esetén $$\rho(x,y)=\frac{2M}{l^{2}\,\mbox{tg}\,\alpha}\,.$$ Így a lejtő tömegközéppontja az $$x_{M}=\frac{l}{3}$$ helyen van. | + | <wlatex>#: Rögzítsük a vonatkoztatási rendszert úgy, hogy az $x$- és $y$- tengelyek a lejtő egymásra merőleges oldalaira illeszkednek. Jelöljük $x_{M}$-mel a lejtő tömegközéppontját, amelyet bizonyos esetekben meg is tudnánk határozni, azonban a számolás során nem lesz szükség a pontos értékére. A teljes rendszer tömegközéppontja $$x_{\mathrm{TKP}}=\frac{0\cdot m+ x_{M} M}{m+M}\,,$$ amely a mozgás során nem változik, hiszen nincs súrlódás az asztal és a lejtő között, így nem hat semmilyen vízszintes irányú külső erő a rendszerre. Ha a lecsúszás után a lejtő $d$ távolságra tolódott el negatív irányba, akkor a rajta lévő $m$ tömegű test az $l-d$ pozícióba kerül. A végállapotban a tömegközéppont helye $$x_{\mathrm{TKP}}=\frac{m(l-d)+M\left(x_{M}-d\right)}{m+M}\,.$$ A két egyenletet összevetve $$d=\frac{m}{m+M}l$$ adódik függetlenül attól, hogy a lejtő homogén-e vagy sem. <br> <br> Megjegyzés: Homogén lejtő esetén ki lehetne számolni a lejtő tömegközéppontjának helyzetét az alábbi számolás szerint. A kezdeti állapotban $$x_{M}=\frac{1}{M}\int_{0}^{l}\int_{0}^{l\,\mbox{tg}\,\alpha\left(1-\frac{x}{l}\right)}\rho(x,y) x dy dx\,,$$ ahol $\rho(x,y)$ a lejtő sűrűsége. Homogén lejtő esetén $$\rho(x,y)=\frac{2M}{l^{2}\,\mbox{tg}\,\alpha}\,.$$ Így a lejtő tömegközéppontja az $$x_{M}=\frac{l}{3}$$ helyen van. |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. augusztus 27., 18:57-kori változata
Feladat
- (3.1.14) Egy súrlódásmentes asztalon
 hajlásszögű,
hajlásszögű,  hosszúságú,
hosszúságú,  tömegű lejtő van. A lejtő tetején egy
tömegű lejtő van. A lejtő tetején egy  tömegű test van. Mekkora távolságra mozdul el a lejtő azalatt míg a test a lejtő aljára csúszik le?
tömegű test van. Mekkora távolságra mozdul el a lejtő azalatt míg a test a lejtő aljára csúszik le?
Megoldás
- Rögzítsük a vonatkoztatási rendszert úgy, hogy az
 - és
- és  - tengelyek a lejtő egymásra merőleges oldalaira illeszkednek. Jelöljük
- tengelyek a lejtő egymásra merőleges oldalaira illeszkednek. Jelöljük 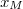 -mel a lejtő tömegközéppontját, amelyet bizonyos esetekben meg is tudnánk határozni, azonban a számolás során nem lesz szükség a pontos értékére. A teljes rendszer tömegközéppontja amely a mozgás során nem változik, hiszen nincs súrlódás az asztal és a lejtő között, így nem hat semmilyen vízszintes irányú külső erő a rendszerre. Ha a lecsúszás után a lejtő
-mel a lejtő tömegközéppontját, amelyet bizonyos esetekben meg is tudnánk határozni, azonban a számolás során nem lesz szükség a pontos értékére. A teljes rendszer tömegközéppontja amely a mozgás során nem változik, hiszen nincs súrlódás az asztal és a lejtő között, így nem hat semmilyen vízszintes irányú külső erő a rendszerre. Ha a lecsúszás után a lejtő![\[x_{\mathrm{TKP}}=\frac{0\cdot m+ x_{M} M}{m+M}\,,\]](/images/math/9/a/1/9a19db904683ce17ad5c3d4fb403fd07.png)
 távolságra tolódott el negatív irányba, akkor a rajta lévő
távolságra tolódott el negatív irányba, akkor a rajta lévő  tömegű test az
tömegű test az 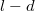 pozícióba kerül. A végállapotban a tömegközéppont helye A két egyenletet összevetve
pozícióba kerül. A végállapotban a tömegközéppont helye A két egyenletet összevetve![\[x_{\mathrm{TKP}}=\frac{m(l-d)+M\left(x_{M}-d\right)}{m+M}\,.\]](/images/math/4/a/7/4a74fa58d10b2ed7304b97f7fd981d06.png) adódik függetlenül attól, hogy a lejtő homogén-e vagy sem.
adódik függetlenül attól, hogy a lejtő homogén-e vagy sem.![\[d=\frac{m}{m+M}l\]](/images/math/7/9/3/79347b10fe7ff34d47474eda1e446f78.png)
Megjegyzés: Homogén lejtő esetén ki lehetne számolni a lejtő tömegközéppontjának helyzetét az alábbi számolás szerint. A kezdeti állapotbanahol![\[x_{M}=\frac{1}{M}\int_{0}^{l}\int_{0}^{l\,\mbox{tg}\,\alpha\left(1-\frac{x}{l}\right)}\rho(x,y) x dy dx\,,\]](/images/math/f/8/9/f89a5e7a3b24e344537fa1f6d054e94f.png)
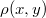 a lejtő sűrűsége. Homogén lejtő esetén Így a lejtő tömegközéppontja az
a lejtő sűrűsége. Homogén lejtő esetén Így a lejtő tömegközéppontja az![\[\rho(x,y)=\frac{2M}{l^{2}\,\mbox{tg}\,\alpha}\,.\]](/images/math/2/9/f/29f0251c4b0002b57d7559d75cb49012.png) helyen van.
helyen van.![\[x_{M}=\frac{l}{3}\]](/images/math/c/f/9/cf9b3e58994feb07cde3d18b97c349dd.png)
- Rögzítsük a vonatkoztatási rendszert úgy, hogy az