„Pontrendszerek - 3.3.1” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Pontrendszerek {{Kísérleti fizika gyakorl…”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Lövedékek sebességének mérésére az ún. ballisztikus ingát használják. A homokkal töltött $M=100\,\mathrm{kg}$ tömegű inga $m=0,2\,\mathrm{kg}$-os lövedék becsapódása után $10^\circ$-kal kilendül. Mekkora a lövedék sebessége? Az inga súlypontjának a felfüggesztési ponttól való távolsága $l=2\,\mathrm{m}$. | + | </noinclude><wlatex># (3.3.1) Lövedékek sebességének mérésére az ún. ballisztikus ingát használják. A homokkal töltött $M=100\,\mathrm{kg}$ tömegű inga $m=0,2\,\mathrm{kg}$-os lövedék becsapódása után $10^\circ$-kal kilendül. Mekkora a lövedék sebessége? Az inga súlypontjának a felfüggesztési ponttól való távolsága $l=2\,\mathrm{m}$. |
</wlatex><includeonly><wlatex>{{Útmutatás|content=Tökéletesen rugalmatlan ütközés.}}{{Végeredmény|content=$v=1560 \,\mathrm{\frac{m}{s}}$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=Tökéletesen rugalmatlan ütközés.}}{{Végeredmény|content=$v=1560 \,\mathrm{\frac{m}{s}}$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap jelenlegi, 2013. augusztus 27., 21:41-kori változata
Feladat
- (3.3.1) Lövedékek sebességének mérésére az ún. ballisztikus ingát használják. A homokkal töltött
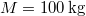 tömegű inga
tömegű inga 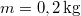 -os lövedék becsapódása után
-os lövedék becsapódása után 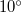 -kal kilendül. Mekkora a lövedék sebessége? Az inga súlypontjának a felfüggesztési ponttól való távolsága
-kal kilendül. Mekkora a lövedék sebessége? Az inga súlypontjának a felfüggesztési ponttól való távolsága 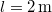 .
.
Megoldás
- A lövedék és a homokzsák tökéletesen rugalmatlan ütközést szenvednek, melynek során a közös végsebesség
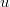 lesz. Az impulzus megmaradás miatt Az ütközés után a homokzsák és a lövedék kilendül, melynek során a kezdeti kinetikus energia helyzeti energiává alakul.
lesz. Az impulzus megmaradás miatt Az ütközés után a homokzsák és a lövedék kilendül, melynek során a kezdeti kinetikus energia helyzeti energiává alakul.![\[(M+m)u=mv\,.\]](/images/math/8/8/5/88523cfd6871d0ba0f577c32741d5c1e.png) Ezzel a korábbi egyenletbe helyettesítve
Ezzel a korábbi egyenletbe helyettesítve![\[\frac{1}{2}(M+m)u^{2}=(M+m)gl(1-\cos\alpha)\qquad\Rightarrow\qquad u=\sqrt{2gl(1-\cos\alpha)}\]](/images/math/7/1/5/7153f003930760305c0c697c251834b9.png)
![\[v=\left(1+\frac{M}{m}\right)\sqrt{2gl(1-\cos\alpha)}=1560 \,\mathrm{\frac{m}{s}}\,.\]](/images/math/a/9/a/a9ad12a41ea68a9dc867c01e11cfaeb3.png)
- A lövedék és a homokzsák tökéletesen rugalmatlan ütközést szenvednek, melynek során a közös végsebesség