„Pontrendszerek - 3.1.9” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
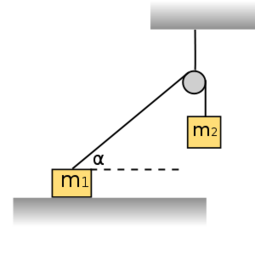
| − | </noinclude><wlatex># (3.1.9) Vízszintes talajon $m_{1}=40\,\mathrm{kg}$ tömegű láda fekszik, a súrlódási együttható $\mu=0,2$. Mekkora $m_{2}$ tömegű test képes a ládát megmozdítani az ábrán látható elrendezésben? Mekkora pillanatnyi gyorsulással indulna el ilyen $m_{2}$ tömeg hatására a láda egy súrlódásmentes vízszintes síkon? A csiga tömegét és súrlódását a számításokban elhanyagolhatjuk. ($\alpha=30^\circ$)[[Kép:Kfgy1_3_1_9.svg|none|255px]] </wlatex><includeonly><wlatex>{{Útmutatás|content=A tapadás feltétele, hogy a tapadási súrlódási erő felső korlátját $T\leq \mu N$ szerint adhatjuk meg.}}{{Végeredmény|content= $m_{2}> 8,28\,\mathrm{kg}$ <br> $a=1, | + | </noinclude><wlatex># (3.1.9) Vízszintes talajon $m_{1}=40\,\mathrm{kg}$ tömegű láda fekszik, a súrlódási együttható $\mu=0,2$. Mekkora $m_{2}$ tömegű test képes a ládát megmozdítani az ábrán látható elrendezésben? Mekkora pillanatnyi gyorsulással indulna el ilyen $m_{2}$ tömeg hatására a láda egy súrlódásmentes vízszintes síkon? A csiga tömegét és súrlódását a számításokban elhanyagolhatjuk. ($\alpha=30^\circ$)[[Kép:Kfgy1_3_1_9.svg|none|255px]] </wlatex><includeonly><wlatex>{{Útmutatás|content=A tapadás feltétele, hogy a tapadási súrlódási erő felső korlátját $T\leq \mu N$ szerint adhatjuk meg.}}{{Végeredmény|content= $m_{2}> 8,28\,\mathrm{kg}$ <br> $a=1,52\,\mathrm{\frac{m}{s^{2}}}$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Vizsgáljuk meg, hogy mi a feltétele annak, hogy az $m_{1}$ tömegű test ne mozduljon el. A rá ható erők az $F_{g}$ gravitációs erő, $N$ nyomóerő, $T$ tapadási súrlódási erő és a kötél által kifejtett $K$ kötélerő, melynek iránya a vízszintessel $\alpha$ szöget zár be. A kötélerőt felbontjuk vízszintes ($K\cos\alpha$) és függőleges ($K\sin\alpha$) komponensekre. Az $m_{1}$ tömegű testre vonatkozó függőleges és vízszintes irányú mozgásegyenletek $$K\sin\alpha+N=m_{1}g\qquad\qquad K\cos\alpha=T\,.$$ Az $m_{2}$ tömegű test sem mozdul ebben az esetben, így $K=m_{2}g$. A tapadási súrlódási erő és a nyomóerő között teljesülnie kell az alábbi összefüggésnek. $$T\leq \mu N$$ $$m_{2}\leq \frac{\mu}{\cos\alpha+\mu\sin\alpha}m_{1}$$ Ez a feltétel azt adja meg, hogy mekkorának kell lennie az $m_{2}$ tömegű testnek ahhoz, hogy az $m_{1}$ tömegű ne mozduljon el. Ha ennek ellenkezőjére vagyunk kíváncsiak, vagyis arra, hogy mekkora $m_{2}$ kell ahhoz, hogy $m_{1}$ elmozduljon, akkor nyilvánvalóan $$m_{2}> \frac{\mu}{\cos\alpha+\mu\sin\alpha}m_{1}=8,28\,\mathrm{kg}$$ kell, hogy teljesüljön. <br> Ha nem lenne súrlódás és $m_{2}=8,28\,\mathrm{kg}$ lenne, akkor az $m_{1}$ tömegű test vízszintes irányú, $a$ nagyságú, míg az $m_{2}$ tömegű test pedig $a\cos\alpha$ gyorsulással indul el. Az $a$ gyorsulás meghatározásához írjuk fel a mozgás egyenleteket. $$m_{1}a=K\cos\alpha$$ $$m_{2}a\cos\alpha=m_{2}g-K$$ A két egyenlet alapján $$a=\frac{m_{2}}{m_{2}\cos\alpha+\frac{m_{1}}{\cos\alpha}}=1, | + | <wlatex>#: Vizsgáljuk meg, hogy mi a feltétele annak, hogy az $m_{1}$ tömegű test ne mozduljon el. A rá ható erők az $F_{g}$ gravitációs erő, $N$ nyomóerő, $T$ tapadási súrlódási erő és a kötél által kifejtett $K$ kötélerő, melynek iránya a vízszintessel $\alpha$ szöget zár be. A kötélerőt felbontjuk vízszintes ($K\cos\alpha$) és függőleges ($K\sin\alpha$) komponensekre. Az $m_{1}$ tömegű testre vonatkozó függőleges és vízszintes irányú mozgásegyenletek $$K\sin\alpha+N=m_{1}g\qquad\qquad K\cos\alpha=T\,.$$ Az $m_{2}$ tömegű test sem mozdul ebben az esetben, így $K=m_{2}g$. A tapadási súrlódási erő és a nyomóerő között teljesülnie kell az alábbi összefüggésnek. $$T\leq \mu N$$ $$m_{2}\leq \frac{\mu}{\cos\alpha+\mu\sin\alpha}m_{1}$$ Ez a feltétel azt adja meg, hogy mekkorának kell lennie az $m_{2}$ tömegű testnek ahhoz, hogy az $m_{1}$ tömegű ne mozduljon el. Ha ennek ellenkezőjére vagyunk kíváncsiak, vagyis arra, hogy mekkora $m_{2}$ kell ahhoz, hogy $m_{1}$ elmozduljon, akkor nyilvánvalóan $$m_{2}> \frac{\mu}{\cos\alpha+\mu\sin\alpha}m_{1}=8,28\,\mathrm{kg}$$ kell, hogy teljesüljön. <br> Ha nem lenne súrlódás és $m_{2}=8,28\,\mathrm{kg}$ lenne, akkor az $m_{1}$ tömegű test vízszintes irányú, $a$ nagyságú, míg az $m_{2}$ tömegű test pedig $a\cos\alpha$ gyorsulással indul el. Az $a$ gyorsulás meghatározásához írjuk fel a mozgás egyenleteket. $$m_{1}a=K\cos\alpha$$ $$m_{2}a\cos\alpha=m_{2}g-K$$ A két egyenlet alapján $$a=\frac{m_{2}}{m_{2}\cos\alpha+\frac{m_{1}}{\cos\alpha}}g=1,52\,\mathrm{\frac{m}{s^{2}}}$$ gyorsulással indulna el. |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. október 30., 10:51-kori változata
Feladat
- (3.1.9) Vízszintes talajon
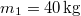 tömegű láda fekszik, a súrlódási együttható
tömegű láda fekszik, a súrlódási együttható 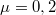 . Mekkora
. Mekkora  tömegű test képes a ládát megmozdítani az ábrán látható elrendezésben? Mekkora pillanatnyi gyorsulással indulna el ilyen
tömegű test képes a ládát megmozdítani az ábrán látható elrendezésben? Mekkora pillanatnyi gyorsulással indulna el ilyen  tömeg hatására a láda egy súrlódásmentes vízszintes síkon? A csiga tömegét és súrlódását a számításokban elhanyagolhatjuk. (
tömeg hatására a láda egy súrlódásmentes vízszintes síkon? A csiga tömegét és súrlódását a számításokban elhanyagolhatjuk. (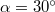 )
)
Megoldás
- Vizsgáljuk meg, hogy mi a feltétele annak, hogy az
 tömegű test ne mozduljon el. A rá ható erők az
tömegű test ne mozduljon el. A rá ható erők az 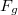 gravitációs erő,
gravitációs erő,  nyomóerő,
nyomóerő,  tapadási súrlódási erő és a kötél által kifejtett
tapadási súrlódási erő és a kötél által kifejtett  kötélerő, melynek iránya a vízszintessel
kötélerő, melynek iránya a vízszintessel  szöget zár be. A kötélerőt felbontjuk vízszintes (
szöget zár be. A kötélerőt felbontjuk vízszintes (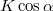 ) és függőleges (
) és függőleges (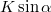 ) komponensekre. Az
) komponensekre. Az  tömegű testre vonatkozó függőleges és vízszintes irányú mozgásegyenletek Az
tömegű testre vonatkozó függőleges és vízszintes irányú mozgásegyenletek Az![\[K\sin\alpha+N=m_{1}g\qquad\qquad K\cos\alpha=T\,.\]](/images/math/1/3/f/13f26bf8dd8c29ffcc0c3cac6f941bbe.png)
 tömegű test sem mozdul ebben az esetben, így
tömegű test sem mozdul ebben az esetben, így 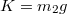 . A tapadási súrlódási erő és a nyomóerő között teljesülnie kell az alábbi összefüggésnek.
. A tapadási súrlódási erő és a nyomóerő között teljesülnie kell az alábbi összefüggésnek. ![\[T\leq \mu N\]](/images/math/7/7/5/7752e5d9457e3df8432246f73c90cb4a.png) Ez a feltétel azt adja meg, hogy mekkorának kell lennie az
Ez a feltétel azt adja meg, hogy mekkorának kell lennie az![\[m_{2}\leq \frac{\mu}{\cos\alpha+\mu\sin\alpha}m_{1}\]](/images/math/a/1/5/a15e1e3ee01412315dc187151b5803c2.png)
 tömegű testnek ahhoz, hogy az
tömegű testnek ahhoz, hogy az  tömegű ne mozduljon el. Ha ennek ellenkezőjére vagyunk kíváncsiak, vagyis arra, hogy mekkora
tömegű ne mozduljon el. Ha ennek ellenkezőjére vagyunk kíváncsiak, vagyis arra, hogy mekkora  kell ahhoz, hogy
kell ahhoz, hogy  elmozduljon, akkor nyilvánvalóan kell, hogy teljesüljön.
elmozduljon, akkor nyilvánvalóan kell, hogy teljesüljön.![\[m_{2}> \frac{\mu}{\cos\alpha+\mu\sin\alpha}m_{1}=8,28\,\mathrm{kg}\]](/images/math/2/3/4/2349b8ccce3addc5920b91e34d06e690.png)
Ha nem lenne súrlódás és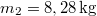 lenne, akkor az
lenne, akkor az  tömegű test vízszintes irányú,
tömegű test vízszintes irányú,  nagyságú, míg az
nagyságú, míg az  tömegű test pedig
tömegű test pedig 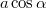 gyorsulással indul el. Az
gyorsulással indul el. Az  gyorsulás meghatározásához írjuk fel a mozgás egyenleteket.
gyorsulás meghatározásához írjuk fel a mozgás egyenleteket. ![\[m_{1}a=K\cos\alpha\]](/images/math/8/b/8/8b898a84d8aa2cb358bec0bde67dcf11.png) A két egyenlet alapján
A két egyenlet alapján![\[m_{2}a\cos\alpha=m_{2}g-K\]](/images/math/d/5/0/d5030430ec6dc80e9878f6340dd51650.png) gyorsulással indulna el.
gyorsulással indulna el.![\[a=\frac{m_{2}}{m_{2}\cos\alpha+\frac{m_{1}}{\cos\alpha}}g=1,52\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/5/3/e/53e3ba7e3396f51af557d571db3d354b.png)
- Vizsgáljuk meg, hogy mi a feltétele annak, hogy az