„Mechanika - Túlcsillapított rezgés” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
(→Feladat) |
||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (**6.30.) Egy $0,5\,\rm{kg}$ tömegű testet olyan rugóra függesztünk, amely $0,1\,\rm N$ erő hatására $8\,\rm{cm}$-rel nyúlik meg. A testre mozgása során sebességével arányos ellenállás hat, amely $0,01\,\rm{\frac ms}$ sebesség esetén $0,05\,\rm N$. A $t=0$ pillanatban a | + | </noinclude><wlatex># (**6.30.) Egy $0,5\,\rm{kg}$ tömegű testet olyan rugóra függesztünk, amely $0,1\,\rm N$ erő hatására $8\,\rm{cm}$-rel nyúlik meg. A testre mozgása során sebességével arányos ellenállás hat, amely $0,01\,\rm{\frac ms}$ sebesség esetén $0,05\,\rm N$. A $t=0$ pillanatban a testet $5\,\rm{cm}$-rel kimozdítjuk egyensúlyi helyzetéből, és kezdősebesség nélkül indítjuk. Határozzuk meg a test mozgását!</wlatex><includeonly><wlatex>{{Útmutatás|content=Állapítsuk meg, hogy a csillapított rezgés melyik alesetéről van szó, és vegyünk fel egy ahhoz illeszkdeő általános megoldást.}}{{Végeredmény|content=$$x(t)=e^{-5t}[0,0527\sinh(4,74t)+0,05\cosh(4,74t)],$$ ahol a számértékek SI alapegységben értendők.}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>A rugóállandó $D=1,25\,\rm{\frac Nm}$, így a csillapítatlan sajátrezgés körfrekvenciája $\omega_0=\sqrt{2,5}\,\frac1{\rm s}$, a közegellenállási erő együtthatója $k=5\,\rm{\frac{Ns}m}$, így a csillapítási tényező $\beta=5\,\frac1{\rm s}$. Mivel $\beta>\omega_0$, a rezgés túlcsillapított. Az ehhez tartozó általános megoldás egyik lehetséges (és praktikus) alakja: $$x(t)=e^{-\beta t}[c_1\sinh(\gamma t)+c_2\cosh(\gamma t)],$$ melyben a $c_1$ és $c_2$ állandókat a kezdeti feltételek határozzák meg, valamint $\gamma=\sqrt{\beta^2-\omega_0^2}=4,74\,\frac1{\rm s}$. $$x(0)=1(c_1 0+c_2 1)=c_2=5\, \rm{cm}$$ $$\dot x(t)=-\beta e^{-\beta t}[c_1\sinh(\gamma t)+c_2\cosh(\gamma t)]+e^{-\beta t}[c_1\gamma\cosh(\gamma t)+c_2\gamma\sinh(\gamma t)]$$ $$\dot x(0)=c_1\gamma-c_2\beta=0,$$ melyből $$c_1=\frac{c_2\beta}{\gamma}=5,27\,\rm{cm}$$</wlatex> | <wlatex>A rugóállandó $D=1,25\,\rm{\frac Nm}$, így a csillapítatlan sajátrezgés körfrekvenciája $\omega_0=\sqrt{2,5}\,\frac1{\rm s}$, a közegellenállási erő együtthatója $k=5\,\rm{\frac{Ns}m}$, így a csillapítási tényező $\beta=5\,\frac1{\rm s}$. Mivel $\beta>\omega_0$, a rezgés túlcsillapított. Az ehhez tartozó általános megoldás egyik lehetséges (és praktikus) alakja: $$x(t)=e^{-\beta t}[c_1\sinh(\gamma t)+c_2\cosh(\gamma t)],$$ melyben a $c_1$ és $c_2$ állandókat a kezdeti feltételek határozzák meg, valamint $\gamma=\sqrt{\beta^2-\omega_0^2}=4,74\,\frac1{\rm s}$. $$x(0)=1(c_1 0+c_2 1)=c_2=5\, \rm{cm}$$ $$\dot x(t)=-\beta e^{-\beta t}[c_1\sinh(\gamma t)+c_2\cosh(\gamma t)]+e^{-\beta t}[c_1\gamma\cosh(\gamma t)+c_2\gamma\sinh(\gamma t)]$$ $$\dot x(0)=c_1\gamma-c_2\beta=0,$$ melyből $$c_1=\frac{c_2\beta}{\gamma}=5,27\,\rm{cm}$$</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. december 3., 14:38-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (**6.30.) Egy
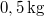 tömegű testet olyan rugóra függesztünk, amely
tömegű testet olyan rugóra függesztünk, amely 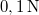 erő hatására
erő hatására 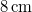 -rel nyúlik meg. A testre mozgása során sebességével arányos ellenállás hat, amely
-rel nyúlik meg. A testre mozgása során sebességével arányos ellenállás hat, amely 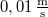 sebesség esetén
sebesség esetén 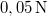 . A
. A  pillanatban a testet
pillanatban a testet 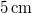 -rel kimozdítjuk egyensúlyi helyzetéből, és kezdősebesség nélkül indítjuk. Határozzuk meg a test mozgását!
-rel kimozdítjuk egyensúlyi helyzetéből, és kezdősebesség nélkül indítjuk. Határozzuk meg a test mozgását!
Megoldás
A rugóállandó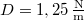 , így a csillapítatlan sajátrezgés körfrekvenciája
, így a csillapítatlan sajátrezgés körfrekvenciája 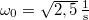 , a közegellenállási erő együtthatója
, a közegellenállási erő együtthatója 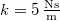 , így a csillapítási tényező
, így a csillapítási tényező 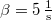 . Mivel
. Mivel 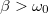 , a rezgés túlcsillapított. Az ehhez tartozó általános megoldás egyik lehetséges (és praktikus) alakja:
, a rezgés túlcsillapított. Az ehhez tartozó általános megoldás egyik lehetséges (és praktikus) alakja: ![\[x(t)=e^{-\beta t}[c_1\sinh(\gamma t)+c_2\cosh(\gamma t)],\]](/images/math/f/f/a/ffabdeda89bdc4ae0e1c0581a83dd2b1.png)
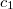 és
és 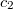 állandókat a kezdeti feltételek határozzák meg, valamint
állandókat a kezdeti feltételek határozzák meg, valamint 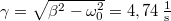 .
. ![\[x(0)=1(c_1 0+c_2 1)=c_2=5\, \rm{cm}\]](/images/math/d/2/b/d2b2abb104429096eb6e3dfcc6524677.png)
![\[\dot x(t)=-\beta e^{-\beta t}[c_1\sinh(\gamma t)+c_2\cosh(\gamma t)]+e^{-\beta t}[c_1\gamma\cosh(\gamma t)+c_2\gamma\sinh(\gamma t)]\]](/images/math/4/a/c/4ac8170a753eedfee69becd011391de9.png)
![\[\dot x(0)=c_1\gamma-c_2\beta=0,\]](/images/math/8/5/8/858f51a78f0481137188830f29272e89.png)
![\[c_1=\frac{c_2\beta}{\gamma}=5,27\,\rm{cm}\]](/images/math/0/d/7/0d7cca6745f74c36625e15a4302d85c1.png)