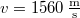„Mechanika - Pontrendszerek” változatai közötti eltérés

A lap 2014. október 18., 12:33-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája: Deriválás Integrálás Mozgástan Erőtan I. Erőtan II. Munka, energia Pontrendszerek Merev testek I. Merev testek II. Rugalmasság, folyadékok Rezgések I. Rezgések II. Hullámok
Mechanika - Pontrendszerek
Feladatok listája: Pontrendszerek - 3.1.2 Pontrendszerek - 3.1.3 Pontrendszerek - 3.1.6 Pontrendszerek - 3.1.7 Pontrendszerek - 3.1.9 Pontrendszerek - 3.1.11 Pontrendszerek - 3.1.12 Pontrendszerek - 3.1.13 Pontrendszerek - 3.1.14 Pontrendszerek - 3.1.16 Pontrendszerek - 3.1.18 Pontrendszerek - Rugalmas ütközés térben Pontrendszerek - 3.1.21 Pontrendszerek - 3.1.23 Pontrendszerek - 3.1.26 Pontrendszerek - 3.3.1
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladatok

(3.1.2) Egy súrlódásmentes álló csigán átvetett fonálon egy 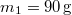$\setbox0\hbox{$m_{1}=90 \,\mathrm{g}$}% \message{//depth:\the\dp0//}% \box0%$ és egy 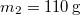$\setbox0\hbox{$m_{2}=110\,\mathrm{g}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test függ. A nehezebb test a földfelszín felett 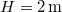$\setbox0\hbox{$H=2\,\mathrm{m}$}% \message{//depth:\the\dp0//}% \box0%$ -re van. Magára hagyva a rendszert, mennyi idő alatt ér le a nagyobb tömegű test a talajra? Feltesszük, hogy a fonál elegendően hosszú. A csiga és a fonál tömegét elhanyagolhatjuk.
Útmutatás
Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!

Végeredmény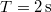
$\setbox0\hbox{$T=2\,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$
Megoldás
(*3.1.3) Egy mozgó csigára egy $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testet függesztünk. A mozgó csigát tartó fonál egyik végét állványhoz erősítjük, másik végét álló csigán átvezetve $\setbox0\hbox{$m_{1}$}% \message{//depth:\the\dp0//}% \box0%$ tömeghez kötjük. Határozzuk meg az $\setbox0\hbox{$m_{1}$}% \message{//depth:\the\dp0//}% \box0%$ , ill. $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömegek gyorsulását! A csigák és a fonál tömegétől, valamint a súrlódástól eltekintünk.

Útmutatás
Írjuk fel a testekre és a csigákra vonatkozó mozgásegyenleteket!

Végeredmény
$a=\frac{4m_{1}-2m_{2}}{4m_{1}+m_{2}}g$

Megoldás
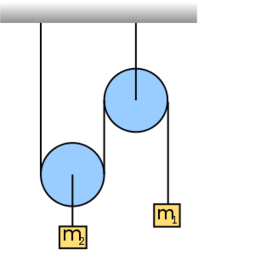
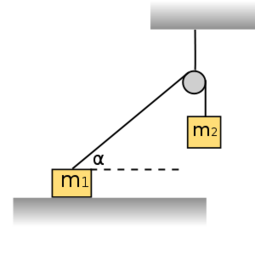
(3.1.6) Egy 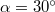$\setbox0\hbox{$\alpha=30^\circ$}% \message{//depth:\the\dp0//}% \box0%$ hajlásszögű lejtőre helyezett 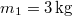$\setbox0\hbox{$m_{1}=3\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testhez a lejtő tetején megerősített csigán átvetett fonállal 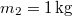$\setbox0\hbox{$m_{2}=1\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testet kötünk. (3.1.6. ábra) Határozzuk meg a rendszer gyorsulását, valamint a fonalat feszítő erőt! Mekkora sebességet ér el a 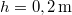$\setbox0\hbox{$h=0,2\,\mathrm{m}$}% \message{//depth:\the\dp0//}% \box0%$ magasságú lejtő tetejéről kezdősebesség nélkül induló test a lejtő alján? A csiga és a fonál tömegétől, valamint a súrlódástól eltekintünk.
Útmutatás
Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!

Végeredmény
$\setbox0\hbox{$a=1,25\,\mathrm{\frac{m}{s^{2}}}\qquad K=11,25\,\mathrm{N}$}% \message{//depth:\the\dp0//}% \box0%$
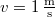
$\setbox0\hbox{$v=1\,\mathrm{\frac{m}{s}}$}% \message{//depth:\the\dp0//}% \box0%$
Megoldás
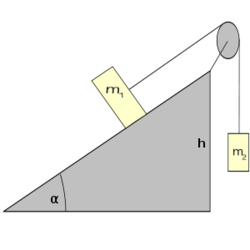
(3.1.7) Kétoldalú lejtő felső pontjában rögzített csigán átvetett fonál egyik végéhez kötött 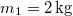$\setbox0\hbox{$m_{1}=2\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test az 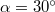$\setbox0\hbox{$\alpha=30^\circ$}% \message{//depth:\the\dp0//}% \box0%$ , másik végéhez kötött 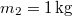$\setbox0\hbox{$m_{2}=1\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test a 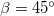$\setbox0\hbox{$\beta=45^\circ$}% \message{//depth:\the\dp0//}% \box0%$ hajlásszögű lejtőn fekszik. Határozzuk meg a gyorsulást és a fonalat feszítő erőt, ha a súrlódástól és a csiga tömegétől eltekintünk!
Útmutatás
Írjuk fel a testekre és a csigára vonatkozó mozgásegyenleteket!

Végeredmény
$\setbox0\hbox{$a=0,976\,\mathrm{\frac{m}{s^{2}}}\qquad\qquad K=8,05\,\mathrm{N}\,.$}% \message{//depth:\the\dp0//}% \box0%$
Megoldás
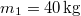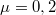(*3.1.9) Vízszintes talajon $\setbox0\hbox{$m_{1}=40\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű láda fekszik, a súrlódási együttható $\setbox0\hbox{$\mu=0,2$}% \message{//depth:\the\dp0//}% \box0%$ . Mekkora $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test képes a ládát megmozdítani az ábrán látható elrendezésben? Mekkora pillanatnyi gyorsulással indulna el ilyen $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömeg hatására a láda egy súrlódásmentes vízszintes síkon? A csiga tömegét és súrlódását a számításokban elhanyagolhatjuk. 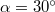( $\setbox0\hbox{$\alpha=30^\circ$}% \message{//depth:\the\dp0//}% \box0%$ )

Útmutatás
A tapadás feltétele, hogy a tapadási súrlódási erő felső korlátját 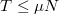$\setbox0\hbox{$T\leq \mu N$}% \message{//depth:\the\dp0//}% \box0%$ szerint adhatjuk meg.

Végeredmény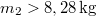
$\setbox0\hbox{$m_{2}> 8,28\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$
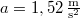
$\setbox0\hbox{$a=1,52\,\mathrm{\frac{m}{s^{2}}}$}% \message{//depth:\the\dp0//}% \box0%$
Megoldás
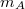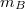(3.1.11) Az $\setbox0\hbox{$m_{A}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű $\setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0%$ és az $\setbox0\hbox{$m_{B}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű $\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$ szabad anyagi pontok Newton törvénye szerint kölcsönösen vonzzák egymást. 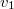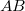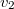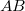A kezdő időpontban az $\setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0%$ pont sebessége $\setbox0\hbox{$v_{1}$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$AB$}% \message{//depth:\the\dp0//}% \box0%$ -re merőleges, $\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$ pont sebessége $\setbox0\hbox{$v_{2}$}% \message{//depth:\the\dp0//}% \box0%$ , $\setbox0\hbox{$AB$}% \message{//depth:\the\dp0//}% \box0%$ irányú és $\setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0%$ -tól elfelé mutat. Határozzuk meg a pontok súlypontjának pályáját és sebességét!
Útmutatás
Számold ki a tömegközéppont sebességét a kezdeti időpillanatban!

Végeredmény
$\mathbf{v}_{TKP}=\frac{1}{m_{A}+m_{B}}\left[\begin{array}{c} m_{A}v_{1} \\ m_{B}v_{2}\end{array}\right]$

Megoldás
(3.1.12) Egy $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú $\setbox0\hbox{$M$}% \message{//depth:\the\dp0//}% \box0%$ tömegű, a vízhez képest nyugvó csónak egyik végén $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű ember áll, majd átmegy a csónak másik végébe. Elhanyagolva a víz ellenállását számítsuk ki, hogy mennyit mozdul el ezalatt a csónak!
Útmutatás
Gondold végig, hogy milyen külső erők hatnak a rendszerre!

Végeredmény
$x=\frac{m}{m+M}l$

Megoldás
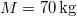(3.1.13) Egy $\setbox0\hbox{$M=70\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű ember kezében 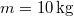$\setbox0\hbox{$m=10\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű teherrel a vízszintessel 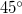$\setbox0\hbox{$45^\circ$}% \message{//depth:\the\dp0//}% \box0%$ -os szöget bezáró irányban 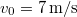$\setbox0\hbox{$v_{0}=7\,\mathrm{m/s}$}% \message{//depth:\the\dp0//}% \box0%$ kezdősebességgel felugrik. Pályája tetőpontján a terhet vízszintes 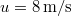$\setbox0\hbox{$u=8\,\mathrm{m/s}$}% \message{//depth:\the\dp0//}% \box0%$ relatív sebességgel hátrafelé hajítja. Mennyivel nagyobb távolságra ugrik ily módon?
Útmutatás
Az eldobás leírásához érdemes figyelembe venni az impulzus megmaradást!

Végeredmény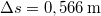
$\setbox0\hbox{$\Delta s=0,566\,\mathrm{m}$}% \message{//depth:\the\dp0//}% \box0%$
Megoldás
(*3.1.14) Egy súrlódásmentes asztalon $\setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0%$ hajlásszögű, $\setbox0\hbox{$M$}% \message{//depth:\the\dp0//}% \box0%$ tömegű lejtő van, amelynek alapja $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszú. A lejtő tetején egy $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test van. Mekkora távolságra mozdul el a lejtő azalatt míg a test a lejtő aljára csúszik le?
Útmutatás
Gondold végig, hogy milyen (irányú) külső erők hatnak a rendszerre!

Végeredmény
$d=\frac{m}{m+M}l$

Megoldás
(3.1.16) Valamely $\setbox0\hbox{$m_{1}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test rugalmatlanul ütközik egy $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test az ütközés előtt nyugalomban volt!
Útmutatás
Tökéletesen rugalmatlan ütközés esetén is érvényes az impulzus megmaradás és a későbbi sebességek azonosak lesznek. Vigyázat! A teljes mozgási energia NEM marad meg az ütközés során!

Végeredmény
$\frac{E_{kin,0}-E_{kin}}{E_{kin,0}}=\frac{m_{2}}{m_{1}+m_{2}}$

Megoldás
(3.1.18) Két rugalmas golyó ugyanakkora $\setbox0\hbox{$v$}% \message{//depth:\the\dp0//}% \box0%$ nagyságú sebességgel halad egymás felé vízszintes egyenesen. Tökéletesen rugalmas ütközés után az egyik golyó nyugalomban marad. Mekkora lesz a másik golyó ütközés előtti és utáni 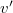$\setbox0\hbox{$v'$}% \message{//depth:\the\dp0//}% \box0%$ sebességeinek aránya? Mekkora a golyók tömegeinek aránya?
Végeredmény
$m_{1}=3m_{2}\qquad\qquad \frac{v'}{v}=2\,.$

Megoldás
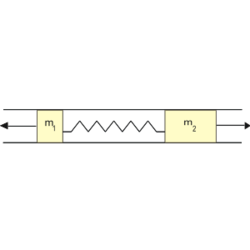
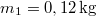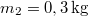(3.1.21) Egy összenyomott rugó hirtelen szétlök két henger alakú tömeget egymással ellentétes irányban. A tömegek nagysága $\setbox0\hbox{$m_{1}=0,12\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$m_{2}=0,3 \,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ . Mekkora sebességgel haladnak ezek a vázolt csőben, ha az összenyomott rugó helyzeti energiája 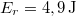$\setbox0\hbox{$E_{r}=4,9\,\mathrm{J}$}% \message{//depth:\the\dp0//}% \box0%$ volt? Hogyan módosul az eredmény, ha az $\setbox0\hbox{$m_{1}$}% \message{//depth:\the\dp0//}% \box0%$ vagy az $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testet a csőben rögzítjük?
Útmutatás
A folyamat során a rugalmas energia mozgaási energiává alakul.

Végeredmény
$v_{1}=12,78\,\mathrm{\frac{m}{s}} \qquad\qquad v_{2}=5,11\,\mathrm{\frac{m}{s}}$

$v_{1}'=9,04\,\mathrm{\frac{m}{s}}$

$v_{2}'=5,76\,\mathrm{\frac{m}{s}}$

Megoldás
(*3.1.23) Egy fonal egyik végét a mennyezethez erősítjük, másik végére $\setbox0\hbox{$m_{1}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testet akasztunk, ehhez egy rugót kötünk, majd a rugóra egy $\setbox0\hbox{$m_{2}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testet. Kezdetben a rendszer nyugalomban van. Ekkor elégetjük a fonalat. Mekkora lesz a testek gyorsulása a következő pillanatban?
Végeredmény
$a_{1}=g\left(1+\frac{m_{2}}{m_{1}}\right)\qquad\qquad a_{2}=0$

Megoldás
(*3.1.26) A rakétát a hajtóműből folytonosan kiáramló gáz gyorsítja. Mennyivel változik az eredetileg 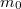$\setbox0\hbox{$m_{0}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű rakéta sebessége, ha a rakétából a rakétához viszonyítva állandó 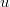$\setbox0\hbox{$u$}% \message{//depth:\the\dp0//}% \box0%$ sebességgel 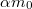$\setbox0\hbox{$\alpha m_{0}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű gáz áramlott ki, ahol 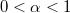$\setbox0\hbox{$0<\alpha<1$}% \message{//depth:\the\dp0//}% \box0%$ ? (A rakétára külső erő nem hat és az 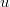$\setbox0\hbox{$u$}% \message{//depth:\the\dp0//}% \box0%$ sebesség a rakéta sebességével ellentétes irányú, de azzal egy egyenesbe esik.)
Útmutatás
Vizsgálja egy általános időpillanatban egy 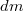$\setbox0\hbox{$dm$}% \message{//depth:\the\dp0//}% \box0%$ infinitezimális tömegű gázmennyiség kilökődését!

Végeredmény
$\Delta v_{\alpha}=-u\ln(1-\alpha)>0$

Megoldás
(3.3.1) Lövedékek sebességének mérésére az ún. ballisztikus ingát használják. A homokkal töltött 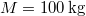$\setbox0\hbox{$M=100\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű inga 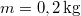$\setbox0\hbox{$m=0,2\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ -os lövedék becsapódása után 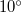$\setbox0\hbox{$10^\circ$}% \message{//depth:\the\dp0//}% \box0%$ -kal kilendül. Mekkora a lövedék sebessége? 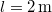Az inga súlypontjának a felfüggesztési ponttól való távolsága $\setbox0\hbox{$l=2\,\mathrm{m}$}% \message{//depth:\the\dp0//}% \box0%$ .
Útmutatás
Tökéletesen rugalmatlan ütközés.

Végeredmény
$\setbox0\hbox{$v=1560 \,\mathrm{\frac{m}{s}}$}% \message{//depth:\the\dp0//}% \box0%$
Megoldás

Pontrendszerek - Rugalmas ütközés síkon

Megoldás

@@ 23. sor: / 23. sor: @@
 {{:Pontrendszerek - 3.1.26}}{{Megoldás|link=Pontrendszerek - 3.1.26}}
 {{:Pontrendszerek - 3.3.1}}{{Megoldás|link=Pontrendszerek - 3.3.1}}
+{{:Pontrendszerek - Rugalmas ütközés síkon}}{{Megoldás|link=Pontrendszerek - Rugalmas ütközés síkon}}

„Mechanika - Pontrendszerek” változatai közötti eltérés

A lap 2014. október 18., 12:33-kori változata

Feladatok

Navigációs menü

Nézetek

Személyes eszközök

navigáció

Képzések

Kísérleti videók

Keresés

Eszközök

Kategóriák