„Pontrendszerek - Rugalmas ütközés térben” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| 11. sor: | 11. sor: | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: | + | <wlatex>#: Az impulzusmegmaradás: $$\vec{p}_0 = \vec{p}_1 + \vec{p}_2 \; .$$ Az energiamegmaradás: $$\frac{1}{2} m v_0^2 = \frac{1}{2} m v_1^2 + \frac{1}{2} m v_2^2 \; . $$ Ezt megszorozva $2m$-mel, és kihasználva, hogy $m v_i = p_i$, az energiamegmaradási egyenlet az alábbi alakot ölti: $$p_0^2 = p_1^2 + p_2^2 \; .$$ Ezt összevetve az impulzusmegmaradásban megjelnő vektorháromszögre azonnal látjuk, hogy a Pitagorasz tétel megfordítása miatt a háromszög derékszögű, tehát $\vec{p}_1$ és $\vec{p}_2$ merőlegesek. |
| + | #: [[Fájl:rajz.svg]] | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. november 10., 22:33-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Pontrendszerek |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
 tömegű részecske vele azonos tömegű, álló részecskének ütközik, rugalmasan. Mutassuk meg, hogy a két részecske ütközés utáni sebességvektorai merőlegesek egymásra!
tömegű részecske vele azonos tömegű, álló részecskének ütközik, rugalmasan. Mutassuk meg, hogy a két részecske ütközés utáni sebességvektorai merőlegesek egymásra!
Megoldás
- Az impulzusmegmaradás: Az energiamegmaradás:
![\[\vec{p}_0 = \vec{p}_1 + \vec{p}_2 \; .\]](/images/math/5/a/0/5a00381876db785c13ea882c34b4ea2f.png) Ezt megszorozva
Ezt megszorozva![\[\frac{1}{2} m v_0^2 = \frac{1}{2} m v_1^2 + \frac{1}{2} m v_2^2 \; . \]](/images/math/b/4/9/b49b2635336031dd36115c9b30483911.png)
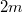 -mel, és kihasználva, hogy
-mel, és kihasználva, hogy 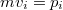 , az energiamegmaradási egyenlet az alábbi alakot ölti: Ezt összevetve az impulzusmegmaradásban megjelnő vektorháromszögre azonnal látjuk, hogy a Pitagorasz tétel megfordítása miatt a háromszög derékszögű, tehát
, az energiamegmaradási egyenlet az alábbi alakot ölti: Ezt összevetve az impulzusmegmaradásban megjelnő vektorháromszögre azonnal látjuk, hogy a Pitagorasz tétel megfordítása miatt a háromszög derékszögű, tehát![\[p_0^2 = p_1^2 + p_2^2 \; .\]](/images/math/7/c/b/7cbc7d7f5cc961495acd8438b0e972f5.png)
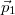 és
és 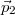 merőlegesek.
merőlegesek.
-
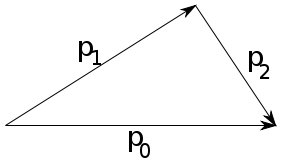
- Az impulzusmegmaradás: