„Mechanika - Szíjhajtás” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
a (→Feladat) |
||
| 10. sor: | 10. sor: | ||
</noinclude><wlatex># (*3.2.17.) Az $m_1$ és $m_2$ tömegű, $R_1$ és $R_2$ sugarú rögzített tengely körül forgó, homogén tömegeloszlású tárcsák elhanyagolható tömegű szíjjal kapcsolódnak egymáshoz. A hajtó tárcsára $M_1$ nagyságú forgatónyomaték hat, a másikat $M_2$ értékű nyomaték terheli. Feltételezzük, hogy a szíj a tárcsákon nem csúszik meg. | </noinclude><wlatex># (*3.2.17.) Az $m_1$ és $m_2$ tömegű, $R_1$ és $R_2$ sugarú rögzített tengely körül forgó, homogén tömegeloszlású tárcsák elhanyagolható tömegű szíjjal kapcsolódnak egymáshoz. A hajtó tárcsára $M_1$ nagyságú forgatónyomaték hat, a másikat $M_2$ értékű nyomaték terheli. Feltételezzük, hogy a szíj a tárcsákon nem csúszik meg. | ||
#: a) Határozzuk meg mindkét tárcsa szöggyorsulását! | #: a) Határozzuk meg mindkét tárcsa szöggyorsulását! | ||
| − | #: b) Hogyan | + | #: b) Hogyan függ az $M_1$ nyomatékot szolgáltató energiaforrás teljesítménye az időtől, ha a $t=0$ időpontban a tárcsák álltak? |
#: c) Milyen teljesítménnyel végez munkát a terhelő szerkezet a $t$-ik időpillanatban? | #: c) Milyen teljesítménnyel végez munkát a terhelő szerkezet a $t$-ik időpillanatban? | ||
#: d) Mire fordítódik az $M_1$ nyomatékot szolgáltató forrás energiájának és a terhelés által végzett munkának a különbsége?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\beta_1=\frac{M_1R_2^2-M_2R_1R_2}{\theta_2R_1^2+\theta_1R_1^2}$$ $$\beta_2=\beta_1\frac{R_1}{R_2}$$ $$P_1=M_1\beta_1t$$ $$P_2=M_2\beta_2t$$}}</wlatex></includeonly><noinclude> | #: d) Mire fordítódik az $M_1$ nyomatékot szolgáltató forrás energiájának és a terhelés által végzett munkának a különbsége?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\beta_1=\frac{M_1R_2^2-M_2R_1R_2}{\theta_2R_1^2+\theta_1R_1^2}$$ $$\beta_2=\beta_1\frac{R_1}{R_2}$$ $$P_1=M_1\beta_1t$$ $$P_2=M_2\beta_2t$$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>A két tárcsa mozgásegyenletének felírásához a két megadott nyomatékon felül a többi nyomatékot is számba kell venni, melyet a szíjat feszítő erők tárcsákra ható ellenerői adnak. A szíj két szakaszát eltérő erő feszíti, így tud mindkét tárcsára eredő nem nulla nyomaték hatni a szíj részéről. Ezt a két erőt $F_1$-el és $F_2$-vel jelölve a nyomatéki mozgásegyenletek: $$\theta_1\beta_1=M_1+(F_1-F_2)R_1$$ és $$\theta_2\beta_2=-M_2+(F_2-F_1)R_2$$ A tömegközéppontok erőegyenleteit ezek megoldásához nem szükséges felírni, annyi többletinformáció adódik belőlük, hogy a tengelyeket tartó erő azonos a két tárcsánál és $T=F_1+F_2$. Ki kell használni azonban, hogy a szíj nem csúszik meg, tehát a két tárcsa kerületi sebessége, így kerületi gyorsulásuk is azonos, ebből adódik a szöggyorsulások viszonyára $\beta_2=\beta_1\frac{R_1}{R_2}$. Ezt a második nyomatéki egyenletbe írva, majd a két egyenletet megfelelő tényezőkkel szorozva elérhető, hogy a tárcsák közti nyomatékátadást leíró tagok a két egyenlet összeadásakor kiesnek, így kapható $$\beta_1=\frac{M_1R_2^2-M_2R_1R_2}{\theta_2R_1^2+\theta_1R_2^2},$$ ebből pedig $\beta_2$. A hatjószerkezet teljesítménye $P_1=M_1\omega_1(t)=M_1\beta_1t$, a terhelő szerkezet munkavégzése pedig $P_2=M_2\omega_2(t)=M_2\beta_2t$. A kettő különbségének idő szerinti integrálja a két tárcsából álló rendszer mozgási energiáját változtatja meg.</wlatex> | <wlatex>A két tárcsa mozgásegyenletének felírásához a két megadott nyomatékon felül a többi nyomatékot is számba kell venni, melyet a szíjat feszítő erők tárcsákra ható ellenerői adnak. A szíj két szakaszát eltérő erő feszíti, így tud mindkét tárcsára eredő nem nulla nyomaték hatni a szíj részéről. Ezt a két erőt $F_1$-el és $F_2$-vel jelölve a nyomatéki mozgásegyenletek: $$\theta_1\beta_1=M_1+(F_1-F_2)R_1$$ és $$\theta_2\beta_2=-M_2+(F_2-F_1)R_2$$ A tömegközéppontok erőegyenleteit ezek megoldásához nem szükséges felírni, annyi többletinformáció adódik belőlük, hogy a tengelyeket tartó erő azonos a két tárcsánál és $T=F_1+F_2$. Ki kell használni azonban, hogy a szíj nem csúszik meg, tehát a két tárcsa kerületi sebessége, így kerületi gyorsulásuk is azonos, ebből adódik a szöggyorsulások viszonyára $\beta_2=\beta_1\frac{R_1}{R_2}$. Ezt a második nyomatéki egyenletbe írva, majd a két egyenletet megfelelő tényezőkkel szorozva elérhető, hogy a tárcsák közti nyomatékátadást leíró tagok a két egyenlet összeadásakor kiesnek, így kapható $$\beta_1=\frac{M_1R_2^2-M_2R_1R_2}{\theta_2R_1^2+\theta_1R_2^2},$$ ebből pedig $\beta_2$. A hatjószerkezet teljesítménye $P_1=M_1\omega_1(t)=M_1\beta_1t$, a terhelő szerkezet munkavégzése pedig $P_2=M_2\omega_2(t)=M_2\beta_2t$. A kettő különbségének idő szerinti integrálja a két tárcsából álló rendszer mozgási energiáját változtatja meg.</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2016. május 11., 12:30-kori változata
Feladat
- (*3.2.17.) Az
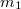 és
és 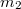 tömegű,
tömegű,  és
és  sugarú rögzített tengely körül forgó, homogén tömegeloszlású tárcsák elhanyagolható tömegű szíjjal kapcsolódnak egymáshoz. A hajtó tárcsára
sugarú rögzített tengely körül forgó, homogén tömegeloszlású tárcsák elhanyagolható tömegű szíjjal kapcsolódnak egymáshoz. A hajtó tárcsára 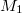 nagyságú forgatónyomaték hat, a másikat
nagyságú forgatónyomaték hat, a másikat 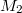 értékű nyomaték terheli. Feltételezzük, hogy a szíj a tárcsákon nem csúszik meg.
értékű nyomaték terheli. Feltételezzük, hogy a szíj a tárcsákon nem csúszik meg.
- a) Határozzuk meg mindkét tárcsa szöggyorsulását!
- b) Hogyan függ az
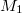 nyomatékot szolgáltató energiaforrás teljesítménye az időtől, ha a
nyomatékot szolgáltató energiaforrás teljesítménye az időtől, ha a  időpontban a tárcsák álltak?
időpontban a tárcsák álltak?
- c) Milyen teljesítménnyel végez munkát a terhelő szerkezet a
 -ik időpillanatban?
-ik időpillanatban?
- d) Mire fordítódik az
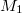 nyomatékot szolgáltató forrás energiájának és a terhelés által végzett munkának a különbsége?
nyomatékot szolgáltató forrás energiájának és a terhelés által végzett munkának a különbsége?
Megoldás
A két tárcsa mozgásegyenletének felírásához a két megadott nyomatékon felül a többi nyomatékot is számba kell venni, melyet a szíjat feszítő erők tárcsákra ható ellenerői adnak. A szíj két szakaszát eltérő erő feszíti, így tud mindkét tárcsára eredő nem nulla nyomaték hatni a szíj részéről. Ezt a két erőt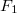 -el és
-el és 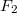 -vel jelölve a nyomatéki mozgásegyenletek:
-vel jelölve a nyomatéki mozgásegyenletek: ![\[\theta_1\beta_1=M_1+(F_1-F_2)R_1\]](/images/math/4/8/0/480e77b9339949659eea3cbc1b732eeb.png)
![\[\theta_2\beta_2=-M_2+(F_2-F_1)R_2\]](/images/math/6/f/6/6f6d16041c6254142d07c6a6a9933a6f.png)
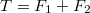 . Ki kell használni azonban, hogy a szíj nem csúszik meg, tehát a két tárcsa kerületi sebessége, így kerületi gyorsulásuk is azonos, ebből adódik a szöggyorsulások viszonyára
. Ki kell használni azonban, hogy a szíj nem csúszik meg, tehát a két tárcsa kerületi sebessége, így kerületi gyorsulásuk is azonos, ebből adódik a szöggyorsulások viszonyára 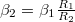 . Ezt a második nyomatéki egyenletbe írva, majd a két egyenletet megfelelő tényezőkkel szorozva elérhető, hogy a tárcsák közti nyomatékátadást leíró tagok a két egyenlet összeadásakor kiesnek, így kapható
. Ezt a második nyomatéki egyenletbe írva, majd a két egyenletet megfelelő tényezőkkel szorozva elérhető, hogy a tárcsák közti nyomatékátadást leíró tagok a két egyenlet összeadásakor kiesnek, így kapható ![\[\beta_1=\frac{M_1R_2^2-M_2R_1R_2}{\theta_2R_1^2+\theta_1R_2^2},\]](/images/math/c/1/7/c173ac5c3c6858a34e5455398ae605be.png)
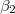 . A hatjószerkezet teljesítménye
. A hatjószerkezet teljesítménye 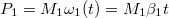 , a terhelő szerkezet munkavégzése pedig
, a terhelő szerkezet munkavégzése pedig 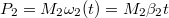 . A kettő különbségének idő szerinti integrálja a két tárcsából álló rendszer mozgási energiáját változtatja meg.
. A kettő különbségének idő szerinti integrálja a két tárcsából álló rendszer mozgási energiáját változtatja meg.