„Mechanika - Egyenletesen gyorsuló forgás” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (3.2.1.) Merev test egyenletesen gyorsuló forgó mozgást végez. Szögsebessége $2\,\mathrm{s}$ alatt $\omega_0=0$-ról $\omega=10\, | + | </noinclude><wlatex># (3.2.1.) Merev test egyenletesen gyorsuló forgó mozgást végez. Szögsebessége $2\,\mathrm{s}$ alatt $\omega_0=0$-ról $\omega=10\,\rm s^{-1}$-ra változik. Mekkora a szöggyorsulása? Mekkora a szögelfordulása $2\,\rm s$ alatt? Mekkora a kerületi gyorsulása a tengelytől $0,2\,\rm m$ távolságra levő tömegpontnak?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\beta=5\,\rm s^{-1}$$ $$\alpha=10\,\rm{rad}$$ $$a=1\,\frac{\rm m}{\rm s^2}$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A szöggyorsulás a szögsebességekből és az eltelt időből $$\beta=\frac{\omega-\omega_0}{t}=5\, | + | <wlatex>A szöggyorsulás a szögsebességekből és az eltelt időből $$\beta=\frac{\omega-\omega_0}{t}=5\,\rm s^{-1}$$ Ezen idő alatt a megtett szögelfordulás $$\alpha=\omega_0t+\frac{\beta}{2}t^2=\omega_{atlag}t=\frac{\omega_0+\omega}{2}t=10\,\rm{rad}$$ A kerületi gyorsulás $$a=\beta R=1\,\frac{{\rm m}}{\rm s^2}$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2012. október 18., 09:18-kori változata
Feladat
- (3.2.1.) Merev test egyenletesen gyorsuló forgó mozgást végez. Szögsebessége
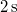 alatt
alatt 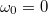 -ról
-ról 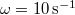 -ra változik. Mekkora a szöggyorsulása? Mekkora a szögelfordulása
-ra változik. Mekkora a szöggyorsulása? Mekkora a szögelfordulása 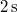 alatt? Mekkora a kerületi gyorsulása a tengelytől
alatt? Mekkora a kerületi gyorsulása a tengelytől 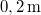 távolságra levő tömegpontnak?
távolságra levő tömegpontnak?
Megoldás
A szöggyorsulás a szögsebességekből és az eltelt időből![\[\beta=\frac{\omega-\omega_0}{t}=5\,\rm s^{-1}\]](/images/math/e/5/7/e573cfa1d80e27026be3d743dd832f9b.png)
![\[\alpha=\omega_0t+\frac{\beta}{2}t^2=\omega_{atlag}t=\frac{\omega_0+\omega}{2}t=10\,\rm{rad}\]](/images/math/9/6/c/96cacd5cc6d88b3e984a36511287058c.png)
![\[a=\beta R=1\,\frac{{\rm m}}{\rm s^2}\]](/images/math/6/5/5/65536317502451341973c5edb25e6259.png)