„Mechanika - Forgatónyomaték gyorsuló forgásnál” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (3.2.2.) Mekkora forgatónyomaték hat arra a $100\,kg\cdot m^2$ tehetetlenségi nyomatékú testre, amely nyugalomból indulva a forgatónyomaték hatására egyenletesen gyorsulva $10\,s$ alatt 50 fordulatot tesz meg?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$M=628\,Nm$$}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex># (3.2.2.) Mekkora forgatónyomaték hat arra a $100\,\rm{kg\cdot m^2}$ tehetetlenségi nyomatékú testre, amely nyugalomból indulva a forgatónyomaték hatására egyenletesen gyorsulva $10\,\rm s$ alatt 50 fordulatot tesz meg?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$M=628\,\rm{Nm}$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A szöggyorsulás $$\beta=\frac{2\alpha}{t^2}=\frac{2\cdot50\cdot2\pi}{100\,s^2}=6,28\,s^{-2}$$ így a forgatónyomaték $M=\theta\beta=628\,Nm$.</wlatex> | + | <wlatex>A szöggyorsulás $$\beta=\frac{2\alpha}{t^2}=\frac{2\cdot50\cdot2\pi}{100\,\rm s^2}=6,28\,\rm s^{-2}$$ így a forgatónyomaték $M=\theta\beta=628\,\rm{Nm}$.</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2012. október 18., 08:21-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek I. |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (3.2.2.) Mekkora forgatónyomaték hat arra a
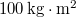 tehetetlenségi nyomatékú testre, amely nyugalomból indulva a forgatónyomaték hatására egyenletesen gyorsulva
tehetetlenségi nyomatékú testre, amely nyugalomból indulva a forgatónyomaték hatására egyenletesen gyorsulva 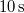 alatt 50 fordulatot tesz meg?
alatt 50 fordulatot tesz meg?
Megoldás
A szöggyorsulás![\[\beta=\frac{2\alpha}{t^2}=\frac{2\cdot50\cdot2\pi}{100\,\rm s^2}=6,28\,\rm s^{-2}\]](/images/math/0/3/f/03fc6d266ed378e67c5d5a113eae0363.png)
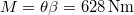 .
.