„Mechanika - Merev testek I.” változatai közötti eltérés
A Fizipedia wikiből
| 12. sor: | 12. sor: | ||
{{:Mechanika - Gömb felületén lévő tengellyel}}{{Megoldás|link=Mechanika - Gömb felületén lévő tengellyel}} | {{:Mechanika - Gömb felületén lévő tengellyel}}{{Megoldás|link=Mechanika - Gömb felületén lévő tengellyel}} | ||
{{:Mechanika - Korong fonállal gyorsítva}}{{Megoldás|link=Mechanika - Korong fonállal gyorsítva}} | {{:Mechanika - Korong fonállal gyorsítva}}{{Megoldás|link=Mechanika - Korong fonállal gyorsítva}} | ||
| + | {{:Mechanika - Pálca mint inga}}{{Megoldás|link=Mechanika - Pálca mint inga}} | ||
| + | {{:Mechanika - Korong mint inga}}{{Megoldás|link=Mechanika - Korong mint inga}} | ||
A lap 2012. november 8., 15:09-kori változata
Feladatok
- (3.2.1.) Merev test egyenletesen gyorsuló forgó mozgást végez. Szögsebessége
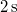alatt 
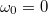-ról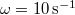 
-ra változik. Mekkora a szöggyorsulása? Mekkora a szögelfordulása 
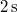alatt? Mekkora a kerületi gyorsulása a tengelytől 
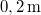távolságra levő tömegpontnak?Végeredmény![\[\beta=5\,\rm s^{-1}\]](/images/math/6/d/e/6de34b1a6a49a8494f2b9c6fc0db1369.png)
![\[\alpha=10\,\rm{rad}\]](/images/math/8/2/5/825c34cc3c15470b5c9142c00945b9c2.png)
![\[a=1\,\frac{\rm m}{\rm s^2}\]](/images/math/a/5/5/a550a7d7899a1174dfaebfa072c8a8b6.png)
- (3.2.2.) Mekkora forgatónyomaték hat arra a
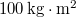tehetetlenségi nyomatékú testre, amely nyugalomból indulva a forgatónyomaték hatására egyenletesen gyorsulva 
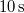alatt 50 fordulatot tesz meg?Végeredmény![\[M=628\,\rm{Nm}\]](/images/math/9/e/b/9eb2134801f4c3896d8a6e575c5ff07a.png)
- (3.2.3.) Egy
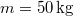és 
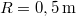sugarú homogén lendítőkerék 
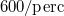fordulatszámmal forog. A korong pereme és a féktuskó között a súrlódási együttható 0,5.
- a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az
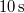alatt megálljon?
- b) Mekkora a megállítás ideje alatt a súrlódó erő munkája?Végeredmény
![\[F=157\,\rm{N}\]](/images/math/2/b/e/2bea2accd3bbd4d30e77898ae3b9d0f7.png)
![\[W_{F_s}=12377\,\rm J=1250\,\pi^2\,\rm J\]](/images/math/d/1/1/d118ed8c66e1bff8b7032653ff3e23a7.png)
- a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az
- (*3.2.4.)
sugarú 
tömegű gömböt egy, sugarának gömbfelület menti végpontján átmenő tengely körül megforgatunk.
- a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan
?
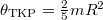- b) Mekkora nyomatékra van szükség ahhoz, hogy
nagyságú szöggyorsulással tudjuk forgásba hozni?
- c) Hogyan kell változni az idő függvényében azon energiaforrás teljesítményének, amely az állandó szöggyorsulást biztosítani képes, ha a gömb a
időpontban nyugalomból indult?Végeredmény![\[\theta=\frac75mR^2.\]](/images/math/9/b/f/9bfcef56b72d5fbd2e1ab88c826a893c.png)
![\[P(t)=\frac75mR^2\beta^2t.\]](/images/math/4/6/7/467595248901aee1cf9b42514dd518c2.png)
- a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan
- (*3.2.5.) Rögzített tengely körül forgó
tömegű és sugarú korong kerületére fonalat csavarunk. A fonalat állandó 
teljesítményű energiaforrással kapcsolatban álló szerkezet feszíti.
- a) Hogyan változik a korong szöggyorsulása az idő függvényében, ha a korong a időpontban nyugalomban volt?
- b) Mennyi ideig kell a fonalat húzni, ha a korong forgási energiáját
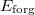értékre akarjuk növelni?Végeredmény![\[\beta=\sqrt{\frac{P}{2\theta}} \frac1{\sqrt t}\]](/images/math/7/6/f/76f2b220a4740349f173edc2d51ce90e.png)
- a) Hogyan változik a korong szöggyorsulása az idő függvényében, ha a korong a
- (*3.2.6.) Mekkora egy
hosszúságú pálca lengésideje, ha a felső végétől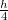 
távolságra levő pontján átmenő tengely körül leng kis szögkitéréssel?ÚtmutatásÍrjuk fel a pálca nyomatéki mozgásegyenletét, majd közelítsük a szögfüggvényeket kis szögekre a Taylor-soruk alapján. A szöggyorsulásra rendezett alakból leolvasható a körfrekvencia négyzete, amiből a lengésidő meghatározható.Végeredmény![\[T=2\pi\sqrt{\frac{7h}{12g}}\]](/images/math/7/b/8/7b81f643792cc1e9067aad908d91ec2b.png)
- (*3.2.7.) Egy tömegű sugarú, homogén tömegeloszlású korong egy kerületi pontján átmenő tengely körül kis szögkitérésű lengéseket végez. A forgástengely a korong homloklapjára merőleges.
- a) Írd fel a korong mozgásegyenletét, mikor az egyensúlyi helyzetéből kimozdult helyzetben van!
- b) Mekkora a korong lengésének periódusideje?ÚtmutatásLásd az előző feladatnál!Végeredmény
![\[T=2\pi\sqrt{\frac{3R}{2g}}\]](/images/math/4/e/a/4ea14b54cee73be1ca8f6026d8c03730.png)
