„Mechanika - Pálca mint inga” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (3.2.6.) Mekkora egy $h$ hosszúságú pálca lengésideje, ha a felső végétől $\frac{h}4$ távolságra levő pontján átmenő tengely körül leng kis szögkitéréssel?</wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a pálca nyomatéki mozgásegyenletét, majd közelítsük a szögfüggvényeket kis szögekre a Taylor-soruk alapján. A szöggyorsulásra rendezett alakból leolvasható a körfrekvencia négyzete, amiből a lengésidő meghatározható.}}{{Végeredmény|content=$$T=2\pi\sqrt{\frac{7h}{12g}}$$}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex># (*3.2.6.) Mekkora egy $h$ hosszúságú pálca lengésideje, ha a felső végétől $\frac{h}4$ távolságra levő pontján átmenő tengely körül leng kis szögkitéréssel?</wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a pálca nyomatéki mozgásegyenletét, majd közelítsük a szögfüggvényeket kis szögekre a Taylor-soruk alapján. A szöggyorsulásra rendezett alakból leolvasható a körfrekvencia négyzete, amiből a lengésidő meghatározható.}}{{Végeredmény|content=$$T=2\pi\sqrt{\frac{7h}{12g}}$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>A megadott forgástengely a tömegközépponttól is $\frac{h}4$ távolságra van, így a Steiner-tétel szerint a rá vonatkozó tehetetlenségi nyomaték $$\theta=\frac1{12}mh^2+m\left(\frac{h}4\right)^2=\frac7{48}mh^2.$$ A végponti tehetetlenségi nyomatékból kiindulni helytelen lett volna, mert sem az, sem a megadott forgáspont nem tömegközéppont! A tömegközéppontban ható súlyerő forgatónyomatéka $$M(\alpha)=mg\frac{h}4sin\alpha\approx mg\frac{h}4\alpha$$ a kis szögek miatt. Ezzel a mozgásegyenlet $$-mg\frac{h}4\alpha=\frac7{48}mh^2\ddot\alpha,$$ egyszerűsítve $$\ddot\alpha=-\frac{12g}{7h}\alpha=-\omega^2\alpha,$$ azaz valóban a harmonikus rezgés mozgásegyenletét kaptuk. Ebből a rezgés körfrekvenciáját leolvasva a periódusidőre adódik $$T=2\pi\sqrt{\frac{7h}{12g}}$$.</wlatex> | <wlatex>A megadott forgástengely a tömegközépponttól is $\frac{h}4$ távolságra van, így a Steiner-tétel szerint a rá vonatkozó tehetetlenségi nyomaték $$\theta=\frac1{12}mh^2+m\left(\frac{h}4\right)^2=\frac7{48}mh^2.$$ A végponti tehetetlenségi nyomatékból kiindulni helytelen lett volna, mert sem az, sem a megadott forgáspont nem tömegközéppont! A tömegközéppontban ható súlyerő forgatónyomatéka $$M(\alpha)=mg\frac{h}4sin\alpha\approx mg\frac{h}4\alpha$$ a kis szögek miatt. Ezzel a mozgásegyenlet $$-mg\frac{h}4\alpha=\frac7{48}mh^2\ddot\alpha,$$ egyszerűsítve $$\ddot\alpha=-\frac{12g}{7h}\alpha=-\omega^2\alpha,$$ azaz valóban a harmonikus rezgés mozgásegyenletét kaptuk. Ebből a rezgés körfrekvenciáját leolvasva a periódusidőre adódik $$T=2\pi\sqrt{\frac{7h}{12g}}$$.</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2012. november 8., 15:16-kori változata
Feladat
- (*3.2.6.) Mekkora egy
hosszúságú pálca lengésideje, ha a felső végétől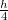 
távolságra levő pontján átmenő tengely körül leng kis szögkitéréssel?
Megoldás
A megadott forgástengely a tömegközépponttól is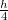 távolságra van, így a Steiner-tétel szerint a rá vonatkozó tehetetlenségi nyomaték ![\[\theta=\frac1{12}mh^2+m\left(\frac{h}4\right)^2=\frac7{48}mh^2.\]](/images/math/f/b/5/fb5fd6b09494ec3026f2e243174c02ef.png)
![\[M(\alpha)=mg\frac{h}4sin\alpha\approx mg\frac{h}4\alpha\]](/images/math/a/7/e/a7e1b7ab57f65e5627abd02c0c611382.png)
![\[-mg\frac{h}4\alpha=\frac7{48}mh^2\ddot\alpha,\]](/images/math/7/1/c/71cdebe49ee69efab675895e7eeeb0a7.png)
![\[\ddot\alpha=-\frac{12g}{7h}\alpha=-\omega^2\alpha,\]](/images/math/b/1/e/b1e4fcc3e02b290723beca9d22060304.png)
![\[T=2\pi\sqrt{\frac{7h}{12g}}\]](/images/math/7/b/8/7b81f643792cc1e9067aad908d91ec2b.png)
