„Mechanika - Korong mint inga” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (3.2. | + | </noinclude><wlatex># (*3.2.7.) Egy $m$ tömegű $R$ sugarú, homogén tömegeloszlású korong egy kerületi pontján átmenő tengely körül kis szögkitérésű lengéseket végez. A forgástengely a korong homloklapjára merőleges. |
| + | #: a) Írd fel a korong mozgásegyenletét, mikor az egyensúlyi helyzetéből kimozdult helyzetben van! | ||
| + | #: b) Mekkora a korong lengésének periódusideje?</wlatex><includeonly><wlatex>{{Útmutatás|content=Lásd az előző feladatnál!}}{{Végeredmény|content=$$T=2\pi\sqrt{\frac{3R}{2g}}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>A tehetetlenségi nyomaték a megadott forgástengelyre vonatkoztatva $$\theta=\frac12mR^2+mR^2=\frac32mR^2.$$ A mozgásegyenlet a kis szögekre közelített forgatónyomatékból $$-mgR\alpha=\frac32mR^2\ddot\alpha,$$, melyet $\ddot\alpha$-ra rendezve leolvasható a körfrekvencia, végül a lengés periódusideje $$T=2\pi\sqrt{\frac{3R}{2g}}$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2012. november 8., 15:19-kori változata
Feladat
- (*3.2.7.) Egy
tömegű 
sugarú, homogén tömegeloszlású korong egy kerületi pontján átmenő tengely körül kis szögkitérésű lengéseket végez. A forgástengely a korong homloklapjára merőleges.
- a) Írd fel a korong mozgásegyenletét, mikor az egyensúlyi helyzetéből kimozdult helyzetben van!
- b) Mekkora a korong lengésének periódusideje?
Megoldás
A tehetetlenségi nyomaték a megadott forgástengelyre vonatkoztatva![\[\theta=\frac12mR^2+mR^2=\frac32mR^2.\]](/images/math/b/2/4/b241d91695c56964b17d7a6be57402d7.png)
![\[-mgR\alpha=\frac32mR^2\ddot\alpha,\]](/images/math/2/a/1/2a14fd1bef8d0a7f892becbdf10a520f.png)
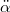-ra rendezve leolvasható a körfrekvencia, végül a lengés periódusideje ![\[T=2\pi\sqrt{\frac{3R}{2g}}\]](/images/math/4/e/a/4ea14b54cee73be1ca8f6026d8c03730.png)
