„Mechanika - Súrlódó tárcsák” változatai közötti eltérés
A Fizipedia wikiből
| 12. sor: | 12. sor: | ||
#: b) Milyen értékűvé válik ez idő alatt a rendszer kinetikus energiája? | #: b) Milyen értékűvé válik ez idő alatt a rendszer kinetikus energiája? | ||
#: c) Ellenőrizze az eredő impulzusmomentum megmaradását! Mi a megmaradás feltétele? | #: c) Ellenőrizze az eredő impulzusmomentum megmaradását! Mi a megmaradás feltétele? | ||
| − | #: d) Milyen súrlódási tényező lenne energiatakarékosság szempontjából gazdaságos?</wlatex><includeonly><wlatex>{{Útmutatás|content= | + | #: d) Milyen súrlódási tényező lenne energiatakarékosság szempontjából gazdaságos?</wlatex><includeonly><wlatex>{{Útmutatás|content=Határozzuk meg a szüggyörsulásokat, majd vizsgáljuk meg, hogy mikor válnak egyenlővé a kerületi sebességek.}}{{Végeredmény|content=$$t=\frac{\omega_0R_1m_1m_2}{2\mu F(m_1+m_2)}$$ $$\omega_1=\omega_0\frac{m_1}{m_1+m_2}$$ $$\omega_2=\omega_0\frac{R_1}{R_2}\frac{m_1}{m_1+m_2}$}}$$ $$E=\frac14\omega_0R_1\frac{m_1}{m_1+m_2}(m_1R_1+m_2R_2)$$ $$\Delta L=\frac12\frac{m_1m_2\omega_0(R_2R_1-R_1^2)}{m_1+m_2}$$ Ez csak azonos sugarak esetén nulla. A súrlódási együttható teszőleges nem nulla érték lehet.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>Mivel csúszási súrlódási erő hat, ennek nagysága ismert $F_s=\mu F$, és a két tárcsa közötti kölcsönhatást erőpárban valósítja meg a III. axióma szerint. Ezen erők nyomatéka a tárcsákon mindaddig hat, amíg az együttforgás be nem áll, azaz a tárcsák kerületi sebessége azonos nem lesz. Ekkor a csúszás megszűnik, és az együttforgás nulla tapadási súrlódási erővel fenntartható. A mozgásegyenletek: $$\theta_1\beta_1=-F_sR_1$$ illetve $$\theta_2\beta_2=+F_sR_2,$$ így a szöggyorsulások $\beta_1=-\frac{2 \mu F}{m_1R_1}$ és $\beta_2=\frac{2 \mu F}{m_2R_2}$. Ezzel a kerületi sebességek $$v_1(t)=R_1 (\omega_0+\beta_1t)$$ és $$v_2(t)=R_2 (\beta_2t),$$ melyek egyenlővé téve megadják a közös forgás létrejöttének idejét $$t=\frac{\omega_0R_1m_1m_2}{2\mu F(m_1+m_2)}$$ Ezt visszahelyettesítve kapjuk a szögsebességeket ebben az állapotban: $\omega_1=\omega_0\frac{m_1}{m_1+m_2}$ és $\omega_2=\omega_0\frac{R_1}{R_2}\frac{m_1}{m_1+m_2}$. Érdemes megjegyezni, hogy bár a beállás ideje függ a súrlódási együtthatótól, a végállapot maga nem, tehát energetikailag a súrlódási együttható értéke ($\mu=0$-t kivéve) közömbös! A mozgási energia: $$E=\frac14\omega_0R_1\frac{m_1}{m_1+m_2}(m_1R_1+m_2R_2),$$ az impulzusmomentum pedig $$L=\frac12\omega_0\frac{m_1}{m_1+m_2}(m_1R_1^2+m_2R_1R_2),$$ amely nem egyezik a kezdeti $$L_0=\frac12m_1R_1^2\omega_0$$ értékkel. Az impulzusmomentum megváltozását képezhetjük e kettő különbségéből, vagy a $\Delta L=\dot Lt$ összefüggéssel felhasználva, hogy $$\dot L=M_1+M_2=F_s(R_2-R_1),$$ így $$\Delta L=\frac12\frac{m_1m_2\omega_0(R_2R_1-R_1^2)}{m_1+m_2}$$ Látható, hogy az impulzusmomentum csak akkor marad meg, ha a tárcsák sugara azonos, így a belső (ez esetben súrlódási) erők eredő nyomatéka is nulla.</wlatex> | <wlatex>Mivel csúszási súrlódási erő hat, ennek nagysága ismert $F_s=\mu F$, és a két tárcsa közötti kölcsönhatást erőpárban valósítja meg a III. axióma szerint. Ezen erők nyomatéka a tárcsákon mindaddig hat, amíg az együttforgás be nem áll, azaz a tárcsák kerületi sebessége azonos nem lesz. Ekkor a csúszás megszűnik, és az együttforgás nulla tapadási súrlódási erővel fenntartható. A mozgásegyenletek: $$\theta_1\beta_1=-F_sR_1$$ illetve $$\theta_2\beta_2=+F_sR_2,$$ így a szöggyorsulások $\beta_1=-\frac{2 \mu F}{m_1R_1}$ és $\beta_2=\frac{2 \mu F}{m_2R_2}$. Ezzel a kerületi sebességek $$v_1(t)=R_1 (\omega_0+\beta_1t)$$ és $$v_2(t)=R_2 (\beta_2t),$$ melyek egyenlővé téve megadják a közös forgás létrejöttének idejét $$t=\frac{\omega_0R_1m_1m_2}{2\mu F(m_1+m_2)}$$ Ezt visszahelyettesítve kapjuk a szögsebességeket ebben az állapotban: $\omega_1=\omega_0\frac{m_1}{m_1+m_2}$ és $\omega_2=\omega_0\frac{R_1}{R_2}\frac{m_1}{m_1+m_2}$. Érdemes megjegyezni, hogy bár a beállás ideje függ a súrlódási együtthatótól, a végállapot maga nem, tehát energetikailag a súrlódási együttható értéke ($\mu=0$-t kivéve) közömbös! A mozgási energia: $$E=\frac14\omega_0R_1\frac{m_1}{m_1+m_2}(m_1R_1+m_2R_2),$$ az impulzusmomentum pedig $$L=\frac12\omega_0\frac{m_1}{m_1+m_2}(m_1R_1^2+m_2R_1R_2),$$ amely nem egyezik a kezdeti $$L_0=\frac12m_1R_1^2\omega_0$$ értékkel. Az impulzusmomentum megváltozását képezhetjük e kettő különbségéből, vagy a $\Delta L=\dot Lt$ összefüggéssel felhasználva, hogy $$\dot L=M_1+M_2=F_s(R_2-R_1),$$ így $$\Delta L=\frac12\frac{m_1m_2\omega_0(R_2R_1-R_1^2)}{m_1+m_2}$$ Látható, hogy az impulzusmomentum csak akkor marad meg, ha a tárcsák sugara azonos, így a belső (ez esetben súrlódási) erők eredő nyomatéka is nulla.</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2012. november 21., 15:58-kori változata
Feladat
- (*3.2.16.) Egymással párhuzamosan elhelyezkedő tengely körül foroghat egy
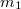 és egy
és egy 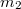 tömegű tárcsa, melyek sugarai rendre
tömegű tárcsa, melyek sugarai rendre  és
és  . Az
. Az  sugarú tárcsát
sugarú tárcsát 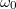 szögsebességgel megforgatjuk, majd az álló
szögsebességgel megforgatjuk, majd az álló  sugarú tárcsához nyomjuk
sugarú tárcsához nyomjuk  erővel. A tárcsák érintkező felületei között a súrlódási együttható
erővel. A tárcsák érintkező felületei között a súrlódási együttható  . ÁBRA
. ÁBRA
- a) Mennyi idő alatt érik el az együttforgás állapotát, és mekkora szögsebességgel forognak ekkor?
- b) Milyen értékűvé válik ez idő alatt a rendszer kinetikus energiája?
- c) Ellenőrizze az eredő impulzusmomentum megmaradását! Mi a megmaradás feltétele?
- d) Milyen súrlódási tényező lenne energiatakarékosság szempontjából gazdaságos?
Megoldás
Mivel csúszási súrlódási erő hat, ennek nagysága ismert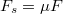 , és a két tárcsa közötti kölcsönhatást erőpárban valósítja meg a III. axióma szerint. Ezen erők nyomatéka a tárcsákon mindaddig hat, amíg az együttforgás be nem áll, azaz a tárcsák kerületi sebessége azonos nem lesz. Ekkor a csúszás megszűnik, és az együttforgás nulla tapadási súrlódási erővel fenntartható. A mozgásegyenletek:
, és a két tárcsa közötti kölcsönhatást erőpárban valósítja meg a III. axióma szerint. Ezen erők nyomatéka a tárcsákon mindaddig hat, amíg az együttforgás be nem áll, azaz a tárcsák kerületi sebessége azonos nem lesz. Ekkor a csúszás megszűnik, és az együttforgás nulla tapadási súrlódási erővel fenntartható. A mozgásegyenletek: ![\[\theta_1\beta_1=-F_sR_1\]](/images/math/3/0/9/309c341d87d1914686f46c9307bf9e3a.png)
![\[\theta_2\beta_2=+F_sR_2,\]](/images/math/8/7/1/871d1e658d8ed648bcd93c7ae371b3e4.png)
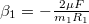 és
és 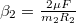 . Ezzel a kerületi sebességek
. Ezzel a kerületi sebességek ![\[v_1(t)=R_1 (\omega_0+\beta_1t)\]](/images/math/2/b/3/2b33834dd995d07c5a1da77398f1a8f9.png)
![\[v_2(t)=R_2 (\beta_2t),\]](/images/math/a/4/e/a4e9ded618697cef9b94cf49ddb745d8.png)
![\[t=\frac{\omega_0R_1m_1m_2}{2\mu F(m_1+m_2)}\]](/images/math/5/e/5/5e52cc73b7a567ae3d2db60e61a8e2c2.png)
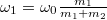 és
és 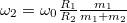 . Érdemes megjegyezni, hogy bár a beállás ideje függ a súrlódási együtthatótól, a végállapot maga nem, tehát energetikailag a súrlódási együttható értéke (
. Érdemes megjegyezni, hogy bár a beállás ideje függ a súrlódási együtthatótól, a végállapot maga nem, tehát energetikailag a súrlódási együttható értéke (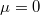 -t kivéve) közömbös! A mozgási energia:
-t kivéve) közömbös! A mozgási energia: ![\[E=\frac14\omega_0R_1\frac{m_1}{m_1+m_2}(m_1R_1+m_2R_2),\]](/images/math/e/7/0/e707e8a8289dd84362a04c3634778d36.png)
![\[L=\frac12\omega_0\frac{m_1}{m_1+m_2}(m_1R_1^2+m_2R_1R_2),\]](/images/math/6/e/c/6ec971609c3244e03a339e57c05ff219.png)
![\[L_0=\frac12m_1R_1^2\omega_0\]](/images/math/a/0/2/a024e5c3cf4000a9b0e04bb5e96e2923.png)
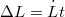 összefüggéssel felhasználva, hogy
összefüggéssel felhasználva, hogy ![\[\dot L=M_1+M_2=F_s(R_2-R_1),\]](/images/math/d/2/3/d23011fa6e9bb6a14f675d9d7156d883.png)
![\[\Delta L=\frac12\frac{m_1m_2\omega_0(R_2R_1-R_1^2)}{m_1+m_2}\]](/images/math/f/c/3/fc3a5cfb7d2f78120e2e0a034d0ac156.png)