„Pontrendszerek - 3.1.21” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy összenyomott rugó hirtelen szétlök két henger alakú tömeget egymással ellentétes irányban. A tömegek nagysága $m_{1}=0,12\,\mathrm{kg}$ és $m_{2}=0,3 \,\mathrm{kg}$. Mekkora sebességgel haladnak ezek a vázolt csőben, ha az összenyomott rugó helyzeti energiája $E_{r}=4,9\,\mathrm{J}$ volt? Hogyan módosul az eredmény, ha az $m_{1}$ vagy az $m_{2}$ tömegű testet a csőben rögzítjük? | + | </noinclude><wlatex># ÁBRA Egy összenyomott rugó hirtelen szétlök két henger alakú tömeget egymással ellentétes irányban. A tömegek nagysága $m_{1}=0,12\,\mathrm{kg}$ és $m_{2}=0,3 \,\mathrm{kg}$. Mekkora sebességgel haladnak ezek a vázolt csőben, ha az összenyomott rugó helyzeti energiája $E_{r}=4,9\,\mathrm{J}$ volt? Hogyan módosul az eredmény, ha az $m_{1}$ vagy az $m_{2}$ tömegű testet a csőben rögzítjük? |
</wlatex><includeonly><wlatex>{{Útmutatás|content=A folyamat során a rugalmas energia mozgaási energiává alakul.}}{{Végeredmény|content=$$v_{1}=12,78\,\mathrm{\frac{m}{s}} \qquad\qquad v_{2}=5,11\,\mathrm{\frac{m}{s}}$$ $$v_{1}'=9,04\,\mathrm{\frac{m}{s}}$$ $$v_{2}'=5,76\,\mathrm{\frac{m}{s}}$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Útmutatás|content=A folyamat során a rugalmas energia mozgaási energiává alakul.}}{{Végeredmény|content=$$v_{1}=12,78\,\mathrm{\frac{m}{s}} \qquad\qquad v_{2}=5,11\,\mathrm{\frac{m}{s}}$$ $$v_{1}'=9,04\,\mathrm{\frac{m}{s}}$$ $$v_{2}'=5,76\,\mathrm{\frac{m}{s}}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap 2013. április 22., 20:01-kori változata
Feladat
- ÁBRA Egy összenyomott rugó hirtelen szétlök két henger alakú tömeget egymással ellentétes irányban. A tömegek nagysága
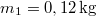és 
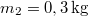. Mekkora sebességgel haladnak ezek a vázolt csőben, ha az összenyomott rugó helyzeti energiája 
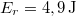volt? Hogyan módosul az eredmény, ha az 
vagy az 
tömegű testet a csőben rögzítjük?
Megoldás
- A szétlökés során nem hat külső erő a két test alkotta pontrendszerre, ezért A szétlökés utáni teljes kinetikus energia megegyezik a szétlökés előtt rugóban tárolt energiával, ha a súrlódás elhanyagolható.
![\[m_{1}v_{1}=m_{2}v_{2}\,.\]](/images/math/1/6/9/169dd422a5d821b8656112d8f590882a.png)
A két egyenletből![\[E_{r}=\frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}\]](/images/math/7/5/1/75193cd13d658206d3c19307dd9a0e73.png)
Ha az egyik test rögzítve van, akkor a rögzítésnél már éri külső erő a rendszert, így az impulzus megmaradás a továbbiakban már nem érvényes. Így a rugóban tárolt energia átalakul valamelyik test teljes mozgási energiájává. Ha az![\[v_{1}=\sqrt{\frac{2E_{r}m_{2}}{m_{1}(m_{1}+m_{2})}}=12,78\,\mathrm{\frac{m}{s}} \qquad\qquad v_{2}=\sqrt{\frac{2E_{r}m_{1}}{m_{2}(m_{1}+m_{2})}}=5,11\,\mathrm{\frac{m}{s}}\,.\]](/images/math/9/3/8/938994332c9117f7c225193f7ce7a723.png)
tömegű testet rögzítjük, akkor a másik test sebessége a szétlökés után. Ha az![\[v_{1}'=\sqrt{\frac{2E_{r}}{m_{1}}}=9,04\,\mathrm{\frac{m}{s}}\]](/images/math/d/7/d/d7d73bc4338aee99933486777a2bd3b4.png)
tömegű testet rögzítjük, akkor a másik test sebessége a szétlökés után.![\[v_{2}'=\sqrt{\frac{2E_{r}}{m_{2}}}=5,76\,\mathrm{\frac{m}{s}}\]](/images/math/0/6/f/06f40a65f3f6a3c00fccc7f6abf9e2a9.png)
- A szétlökés során nem hat külső erő a két test alkotta pontrendszerre, ezért
