Pontrendszerek - 3.1.3
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen SweidanO (vitalap | szerkesztései) 2013. június 29., 18:10-kor történt szerkesztése után volt.
Feladat
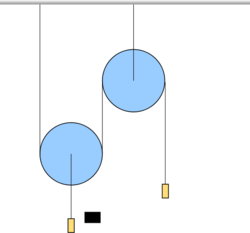
- Egy mozgó csigára egy
 tömegű testet függesztünk. A mozgó csigát tartó fonál egyik végét állványhoz erősítjük, másik végét álló csigán átvezetve
tömegű testet függesztünk. A mozgó csigát tartó fonál egyik végét állványhoz erősítjük, másik végét álló csigán átvezetve  tömeghez kötjük. (3.1.3. ábra) Határozzuk meg az
tömeghez kötjük. (3.1.3. ábra) Határozzuk meg az  , ill.
, ill.  tömegek gyorsulását! A csigák és a fonál tömegétől, valamint a súrlódástól eltekintünk.
tömegek gyorsulását! A csigák és a fonál tömegétől, valamint a súrlódástól eltekintünk.
Megoldás
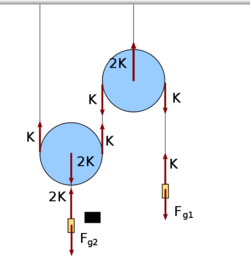
- A csigákra és a testekre ható erőket az ÁBRÁn ábrázoltuk.
 tömegű testre ható kötélerővel. Az állócsiga bal oldalán ható, kötél által kifejtett erő azért egyezik meg a jobb oldalon ható
tömegű testre ható kötélerővel. Az állócsiga bal oldalán ható, kötél által kifejtett erő azért egyezik meg a jobb oldalon ható  erővel, mert a kettő forgatónyomatékának ki kell egyenlítenie egymást. Ez annak a következménye, hogy a csiga tömege zérus, így a tehetetlenségi nyomatéka is zérus, így a forgásokra vonatkozó Newton törvény értelmében az eredő forgatónyomaték is
erővel, mert a kettő forgatónyomatékának ki kell egyenlítenie egymást. Ez annak a következménye, hogy a csiga tömege zérus, így a tehetetlenségi nyomatéka is zérus, így a forgásokra vonatkozó Newton törvény értelmében az eredő forgatónyomaték is 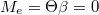 annak ellenére, hogy szöggyorsulása nem
annak ellenére, hogy szöggyorsulása nem  . A mozgó csiga jobb oldalán ható, a kötél által kifejtett erő is
. A mozgó csiga jobb oldalán ható, a kötél által kifejtett erő is  nagyságú, mert az az állócsiga bal oldalán ható erő ellenereje. A mozgócsiga tengelyén ható erő
nagyságú, mert az az állócsiga bal oldalán ható erő ellenereje. A mozgócsiga tengelyén ható erő 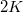 , mert a bal oldalán lévő felfüggesztési pontot tekintve forgástengelynek a csigára ható eredő forgatónyomatéknak zérusnak kell lennie. A csigákra ható erőket a felfüggesztési pontokban a következő megfontolás alapján határoztuk meg. A csigák tömege zérus, ezért a rájuk ható erők eredője is
, mert a bal oldalán lévő felfüggesztési pontot tekintve forgástengelynek a csigára ható eredő forgatónyomatéknak zérusnak kell lennie. A csigákra ható erőket a felfüggesztési pontokban a következő megfontolás alapján határoztuk meg. A csigák tömege zérus, ezért a rájuk ható erők eredője is  kell, hogy legyen. Így a felfüggesztési pontokban kifejtett erőnek ki kell egyensúlyoznia a többi erőt.
kell, hogy legyen. Így a felfüggesztési pontokban kifejtett erőnek ki kell egyensúlyoznia a többi erőt. A fenti érvelésben fontos szerepet játszott az a tény, hogy a csigák és a fonál tömegét elhanyagoltuk, valamint, hogy a fonal nyújthatatlan. A nyújthatatlanságnak az is a következménye, hogy ha az
 tömegű test lefelé gyorsul egy
tömegű test lefelé gyorsul egy  nagyságú gyorsulással, akkor az
nagyságú gyorsulással, akkor az  tömegű test felfelé gyorsul
tömegű test felfelé gyorsul 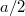 nagyságú gyorsulással. A rájuk vonatkozó mozgásegyenletek:
nagyságú gyorsulással. A rájuk vonatkozó mozgásegyenletek: ![\[m_{1}a=m_{1}g-K\]](/images/math/e/2/3/e23839fbeb3f051da6548c79812a78e7.png)
![\[m_{2}\frac{a}{2}=2K-m_{2}g\]](/images/math/e/e/9/ee91d3b9acea61b84c83126867a2975a.png)
![\[a=\frac{4m_{1}-2m_{2}}{4m_{1}+m_{2}}g\,.\]](/images/math/d/5/4/d541344d8b70a8899ce9a73f5b525f45.png)
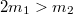 , akkor az
, akkor az  tömegű test fog
tömegű test fog  gyorsulással lefelé, az
gyorsulással lefelé, az  tömegű pedig
tömegű pedig 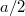 -vel felfelé haladni. Fordított esetben ellenkező irányban történik a mozgás.
-vel felfelé haladni. Fordított esetben ellenkező irányban történik a mozgás.