Mechanika - Korong fonállal gyorsítva
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. november 8., 16:15-kor történt szerkesztése után volt.
Feladat
- (*3.2.5.) Rögzített tengely körül forgó
 tömegű és
tömegű és  sugarú korong kerületére fonalat csavarunk. A fonalat állandó
sugarú korong kerületére fonalat csavarunk. A fonalat állandó  teljesítményű energiaforrással kapcsolatban álló szerkezet feszíti.
teljesítményű energiaforrással kapcsolatban álló szerkezet feszíti.
- a) Hogyan változik a korong szöggyorsulása az idő függvényében, ha a korong a
 időpontban nyugalomban volt?
időpontban nyugalomban volt?
- b) Mennyi ideig kell a fonalat húzni, ha a korong forgási energiáját
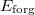 értékre akarjuk növelni?
értékre akarjuk növelni?
- a) Hogyan változik a korong szöggyorsulása az idő függvényében, ha a korong a
Megoldás
Mivel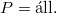 és a test nyugalomból indul,
és a test nyugalomból indul, ![\[E_{\text{forg}}=\frac12\theta\omega^2(t)=Pt\]](/images/math/b/0/c/b0cbc90a0dfbddf02210284ca0b0bb21.png)
![\[\omega(t)=\sqrt{\frac{2P}{\theta}}\sqrt{t},\]](/images/math/2/9/6/296f0d694dd04332b07b1f22014131ba.png)
![\[\beta=\dot\omega=\sqrt{\frac{P}{2\theta}} \frac1{\sqrt t}\]](/images/math/3/4/b/34bb717abeaea3952879922c179dfb11.png)