Pontrendszerek - 3.1.12
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. augusztus 27., 22:39-kor történt szerkesztése után volt.
Feladat
- (3.1.12) Egy
 hosszúságú
hosszúságú  tömegű, a vízhez képest nyugvó csónak egyik végén
tömegű, a vízhez képest nyugvó csónak egyik végén  tömegű ember áll, majd átmegy a csónak másik végébe. Elhanyagolva a víz ellenállását számítsuk ki, hogy mennyit mozdul el ezalatt a csónak!
tömegű ember áll, majd átmegy a csónak másik végébe. Elhanyagolva a víz ellenállását számítsuk ki, hogy mennyit mozdul el ezalatt a csónak!
Megoldás
- Rögzítsük a vonatkoztatási rendszert úgy, hogy az origó abban a pontban van, ahol az ember áll, és a csónak az
 -tengely pozitív felén fekszik. Ebben a koordinátarendszerben a tömegközéppont kezdeti pozíciója ahol
-tengely pozitív felén fekszik. Ebben a koordinátarendszerben a tömegközéppont kezdeti pozíciója ahol![\[x_{\mathrm{TKP}}=\frac{m\cdot 0+M x_{M}}{m+M}\,,\]](/images/math/c/8/2/c82409cc61bc72088b88667768301899.png)
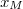 a csónak tömegközéppontja ebben a vonatkoztatási rendszerben. Megjegyezzük, hogy a
a csónak tömegközéppontja ebben a vonatkoztatási rendszerben. Megjegyezzük, hogy a 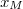 nem feltétlenül egyezik meg
nem feltétlenül egyezik meg 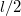 -vel, mert a csónak akár inhomogén is lehet. Látni fogjuk azonban, hogy a pontos értékétől független lesz a megoldás. Amíg az ember átsétál a másik végébe, a teljes rendszer tömegközéppontjának helye nem változik, amennyiben elhanyagoljuk a víz ellenállását. Ha a csónak közben
-vel, mert a csónak akár inhomogén is lehet. Látni fogjuk azonban, hogy a pontos értékétől független lesz a megoldás. Amíg az ember átsétál a másik végébe, a teljes rendszer tömegközéppontjának helye nem változik, amennyiben elhanyagoljuk a víz ellenállását. Ha a csónak közben  -t mozdul el negatív irányba, akkor az ember pozíciója
-t mozdul el negatív irányba, akkor az ember pozíciója 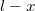 . A vég állapotban A két egyenletet összevetve
. A vég állapotban A két egyenletet összevetve![\[x_{\mathrm{TKP}}=\frac{m\cdot (l-x)+M\left(x_{M}-x\right)}{m+M}\]](/images/math/0/0/3/0039b258f1d34899c747392b5d1552ca.png)
![\[x=\frac{m}{m+M}l\,.\]](/images/math/e/4/8/e4857e674f54a2f230ac08e81658116f.png)
- Rögzítsük a vonatkoztatási rendszert úgy, hogy az origó abban a pontban van, ahol az ember áll, és a csónak az